当今时代,随着交通越来越发达,我们更加愿意选择公共交通出行。然而在去往目的地的时,公共交通有时并不能直达,需要中转。中转有时候会非常浪费时间,因而我们希望在去往目的地的过程中,中转的次数越少越好。以往,我们需要自己记忆繁杂的交通网络人为判断;而现在,我们可以很方便地从手机中的地图app中获取最少中转的方案。你有没有想过,这些最少中转方案是怎么生成的呢?
面对这个问题感觉无从下手?那我们一起来看看地图导航app中是如何简化这个问题的。
地图上,我们自己的位置和目的地的位置被简化为两个不同的点,各个公共交通站台也被简化成一个个点;一条条线连接着不同的点,这意味着这两点可以通过一种公共交通直达。这种由点和线连接起来的结构,在数据结构中叫做“图”。其中的点叫做“顶点”( \(Vertex\) ),线则叫做“边”( \(Edge\) )。
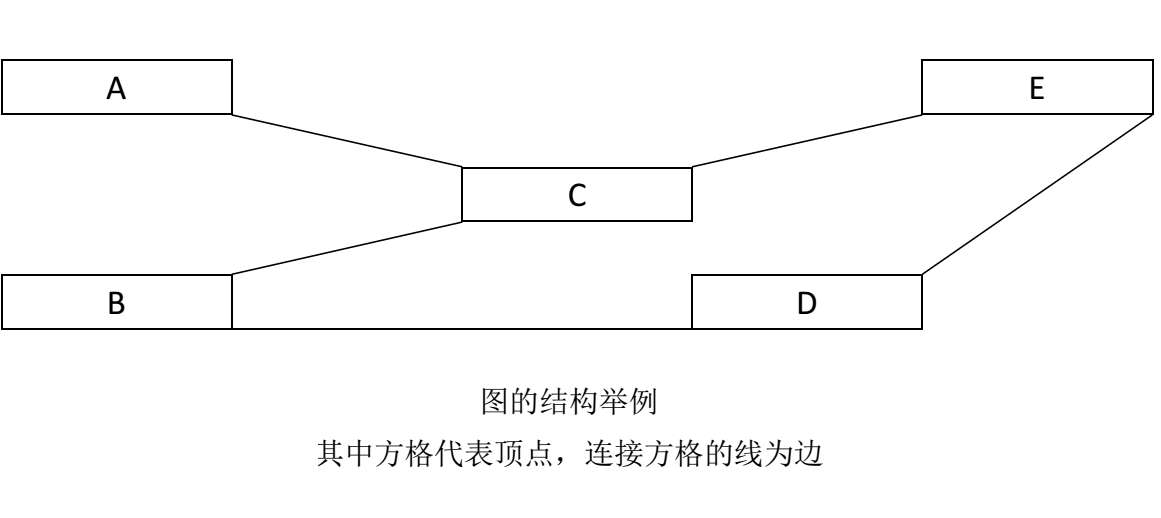
有了“图”这种结构,我们就可以构建出一个简易的交通网络。以此为基础,让我们回到文章开始提出的问题:如何利用这样的信息来寻找最少中转方案呢?
在了解这个算法之前,我们先来了解一下图这个数据结构中的“邻居”的概念。
比如上图中,假设你在 \(C\) 点,那么 \(A\) 、 \(B\) 、 \(E\) 是与你直接相连的,这些顶点也叫做 \(C\) 的“邻居”( \(Neighbour\) )。
利用“邻居”的概念,该算法可以描述如下:
计算机会先寻找你周围的“邻居”,检查这些地点是否是你的目的地。如果是,那么就可以返回结果了;如果不是,那么再依次检查你“邻居”的“邻居”···依次类推,直到找到目的地。
从“邻居”到其自身“邻居”依次遍历,保证自己的位置到目的地是一条可行的通路;按照距离你位置由近到远的“邻居”为顺序依次检查,保证了路径是最短中转。因此,这个算法是有效的。
上述求最少中转方案的算法,其实是图算法中一种遍历算法的具体应用。这种遍历图的算法称作“宽度优先搜索”( \(Breadth-First \ Search\) )。它从一个点出发,先遍历起点周围的未被访问过的“邻居”顶点,再遍历“邻居”顶点的未被访问过的“邻居”顶点···依次类推,直到所有能够被访问到的顶点(也就是该点与起点之间存在一条路径)都被访问过。如果在此过程中,还有未被访问的顶点,那么重新选择一个未被访问的顶点作为新起点,并重复上述操作。
那么这个算法如何实现呢?
在此之前,我们要考虑如何利用编程语言来描述图这种结构。
图在计算机中的存储结构通常有三个,分别是数组表示法(有时候也叫邻接矩阵表示法)、邻接表表示法、十字链表表示法。限于篇幅。我这里只讨论前两种,第三种大家自己找相关书籍阅读吧。 :)
从“数组表示法”的命名,我们很自然地想到利用数组来存储顶点信息;从“邻接矩阵表示法”的命名,我们也可以很自然的想到这种方式是利用矩阵来存储顶点与顶点之间的关联。
假设图中有 \(N\) 个顶点,那么建立一个大小为 \(N\) 的数组存储顶点信息;接下来再创建一个大小为 \(N × N\) 的矩阵存储顶点之间的联系。假设存储在顶点数组下标为 \(i\) 和 \(j\) 的两个顶点直接相连,如果这种相连关系是单向的(比如从 \(i\) 到 \(j\) ),那么矩阵 \(( i, j )\) 位置存储 1 (表示它们是相邻的,而 0 自然是表示它们不相邻);如果这种相连关系是双向的,那么矩阵 \(( j, i )\) 位置上的值也得是 1 。

把我们上面用于举例的图的结构拿过来,我们发现顶点之间的联系是双向的。换句话说,方向在这种图中,是没有意义的。这样顶点双向联系的图叫做“无向图”。依据这点分析,顶点单向联系的图便叫做“有向图”。
面对这个无向图,我们可以很容易得到它的顶点数组和其邻接矩阵。具体如下:
顶点数组:\(\{A,B,C,D,E\}\)
邻接矩阵: \[ \left[\begin{array}{ccc} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 0\\ 1 & 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 1 & 1 & 0\\ \end{array} \right] \] 对应的表格如下:
| · | A | B | C | D | E |
|---|---|---|---|---|---|
| A | 0 | 0 | 1 | 0 | 0 |
| B | 0 | 0 | 1 | 1 | 0 |
| C | 1 | 1 | 0 | 0 | 1 |
| D | 0 | 1 | 0 | 0 | 1 |
| E | 0 | 0 | 1 | 1 | 0 |
仔细观察,我们发现,无向图的邻接矩阵是以主对角线对称的。根据这点特性,对于无向图,我们可以只存储一个上三角区域(或者是下三角区域)来节省存储空间。
上述图的存储方式十分简单,但是如果图中的边非常少,那么邻接矩阵中大部分存储的都是零,造成了极大的空间浪费。怎么解决这个问题呢?
邻接表的存储方式就是来解决这一问题的。邻接表的存储结构有点像我们之前介绍过的数组链表的混合结构。每个链表的表头存储顶点信息,这些链表构成一个链表数组。每个链表表头后续的链表元素存储与表头所存顶点直接相连顶点在链表数组中的下标。

那么上图就可以利用邻接表表示为
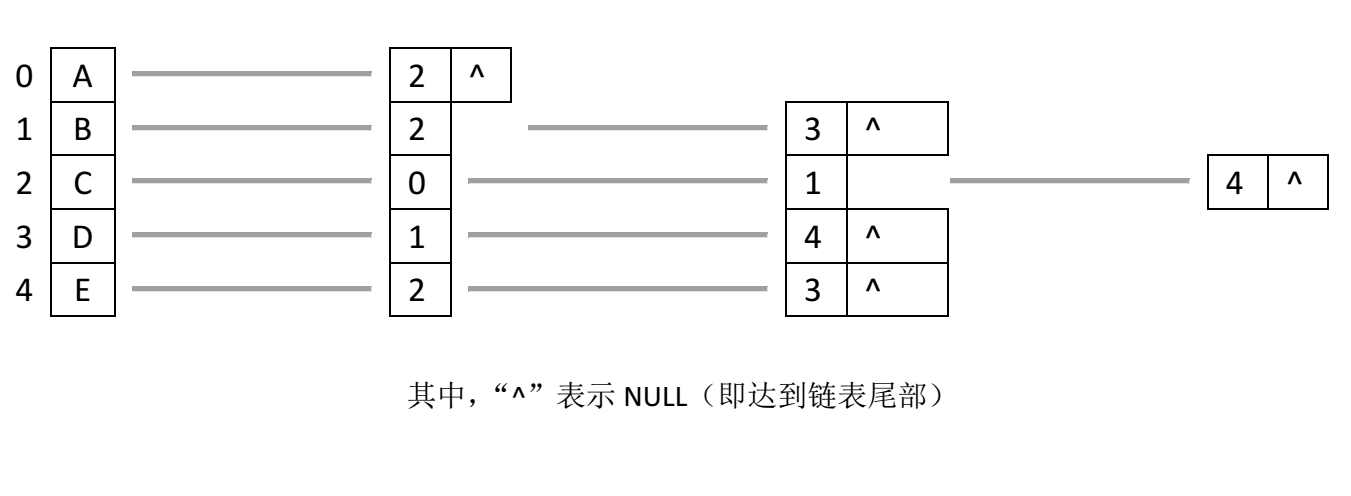
我们对比两者图的存储结构,可以发现,邻接表可以很快获取一个顶点的“邻居”顶点。因而,对于求最短路径算法,我们选择邻接表存储图的信息。
为了图中的顶点能够按照宽度优先搜索时的顺序遍历,我们这里还要利用另一个叫做“队列”数据结构。“队列”,和生活中的排队十分相似,数据在队列中“先进先出”【 \(FIFO\) 】(与之相反,数据在栈中“先进后出”【 \(FILO\) 】)。队列只支持两种操作,一种为 \(EnQueue\) (入队,将元素加入队尾),另一种为 \(DeQueue\) (出队,从队首移除元素,并返回该元素的值)。
从起点开始,依次将其“邻居”顶点加入队列;在遍历“邻居”顶点时,先将该顶点出队,再将“邻居”顶点的“邻居”顶点依次入队···直到找到目的地顶点。如果这个过程结束后,队列为空,那么已知的图上不存在相关路径。
好了,今天就到这里。算法的实现留给大家思考。也许,我之后会补上一篇文章介绍该算法的实现。
最后是本文的总结:
- 利用图这种数据结构可以很全面地描述多个点之间相互关联的信息(比如地图)。
- 利用图的广度优先搜索,我们可以遍历图中的每一个顶点、判断一个顶点到另一个顶点是否存在路径、计算乘坐公交去目的地的最少中转方案等问题。
- 图的存储结构有三种,分别是邻接矩阵表示法、邻接表表示法、十字链表表示法。
- 广度优先搜索中利用到“队列”的数据结构。
- 数据在队列中“先进先出”【 \(FIFO\) 】。队列只支持两种操作,一种为 \(EnQueue\) (入队,将元素加入队尾),另一种为 \(DeQueue\)(出队,从队首移除元素,并返回该元素的值)
- 对比第5点,数据在栈中“先进后出”【 \(FILO\) 】