7．图

图的基本概念；图的存储表示：邻接矩阵、邻接表

基本概念

详细见教材 7.1 节

存储表示

邻接矩阵

存储

// 图的邻接矩阵存储表示

// 用矩阵来存储顶点之间的连接关系

#define INFINITY        INT_MAX              // 最大值 正无穷
#define MAX_VERTEX_NUM  20                   // 最大顶点个数

typedef enum {DG, DN, UDG, UDN} GraphKind;   // {有向图，有向网，无向图。无向网}

typedef struct ArcCell{
    VRType    adj;                           // VRType 是顶点关系类型
                                             // 对无权图：
                                             // 用 1，0 代表相邻否
                                             // 对带权图：
                                             // 为权值类型
    InfoType  *info;                         // 该弧相关信息指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VEXTEX_NUM];

typedef struct{
    VertexType vexs[MAX_VERTEX_NUM];         // 顶点向量
    AdjMatrix  arcs;                         // 邻接矩阵
    int        vexnum, arcnum;               // 图的当前顶点数和弧数
    GraphKind  kind;                         // 图的种类标志
}MGraph;

更适合存储稠密图，容易判定任意两个顶点是否有边连接
顶点度的计算
- 无向图：
\[ TD(v_i) = \sum^{n-1}_{j=0}{A[i][j]},n = MAX\_VERTEX\_NUM（即第 i 行元素之和） \]
- 有向图
\[ OD(v_i) = \sum^{n-1}_{j=0}{A[i][j]},n = MAX\_VERTEX\_NUM（即第 i 行元素之和） \]

\[ ID(v_j) = \sum_{i=0}^{n-1}A[i][j],n = MAX\_VERTEX\_NUM（即第 j 列元素之和） \]
- 对于网，对应度的大小，便是数对应位置的的非 $\infty$ 的个数

邻接表

// 图的邻接表存储表示

// 对图的每一个顶点建立一个单链表，其后连接与之相邻接的顶点
// 每个顶点的单链表的头存储在一个数组中

#define MAX_VERTEX_NUM    20

// 单链表结点定义
typedef struct ArcNode{
    int            adjvex;         // 该弧所指向的顶点的位置
    struct ArcNode *nextarc;       // 指向下一条弧的指针
    InfoType       *info;          // 该弧相关信息的指针
}ArcNode;

// 数组定义（用于存储单链表的头）
typedef struct VNode{
    VertexType    data;            // 顶点信息
    ArcNode       *firstarc;       // 指向第一条依附该顶点的弧的指针
}VNode, AdjList[MAX_VERTEX_NUM];

// 邻接表图的定义
typedef struct{
    AdjList       vertices;
    int           vexnum, arcnum;  // 图的当前顶点数和弧数
    int           kind;            // 图的种类标志
}ALGraph;

更适合存储稀疏图，容易寻找任意一个顶点的第一个邻接点和下一个邻接点。
顶点度的计算
- 无向图：顶点 $v_i$ 的度为第 $i$ 个链表中的结点数（头节点本身不算）
- 有向图：顶点 $v_i$ 的出度为第 $i$ 个链表中的结点数（头节点本身不算）；入度则要遍历整个图
- 对于网，与上述方法对应相同

图的遍历与连通性

遍历

深度优先搜索

// 下面两个算法用到的全局变量

Boolean visited[MAX];         // 访问标志数组
Status (*VisitFunc)(int v);   // 函数变量

// 算法 7.4
// 对图 G 做深度优先遍历

void DFSTraverse(Graph G, Status(* Visit)(int v))
{
    VisitFunc = Visit;
    for(v = 0; v < G.vexnum; ++v)    visited[v] = FALSE; // 标志数组初始化
    for(v = 0; V < G.vexnum; ++ v)
        if(! visited[v])
            DFS(G, v);                                   // 对未访问的顶点调用 DFS
}

// 算法 7.5
// 从第 v 个结点出发，递归的深度优先遍历图 G

void DFS(Graph G, int v)
{
    visited[v] = TRUE;    VisitFunc(v);       // 访问第 v 个顶点
    for(w = FirstAdjVex(G, v); w >= 0; w = nextAdjVex(G, v, w))
        if(! visited[w])
            DFS(G, v);                        // 对 v 尚未访问的邻接顶点 w 递归调用 DFS
}

性能分析
- 空间复杂度：$O( |V| )$，其中$ |V|$ 为顶点数，下同
- 时间复杂度
  - 邻接矩阵存储：$O( |V|^2 )$
  - 邻接表存储：$O(|V|+|E|)$ ，其中 $|E|$ 为边数

广度优先搜索

// 算法 7.6
// 按广度优先非递归遍历图 G。使用辅助队列 Q 和访问数组 visited

void BFSTraverse(Graph G, Status(* Visit)(int v))
{
    for(v = 0; v < G.vexnum; ++v)    visited[v] = FALSE;
    InitQueue(Q);                    // 置空的辅助队列 Q
    for(v = 0; v < G.vexnum; ++v)
        if( !visited[v])             // v 未被访问
        {
            visited[v] = TRUE;    Visit(v);
            EnQueue(Q, v);           // v 入队
            while(! QueueEmpty(Q))
            {
                DeQueue(Q, u);       // 出队，并置为 u
                for(w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w))
                    if(! visited[w]) // w 为 u 的尚未访问的邻接顶点
                    {
                        visited[w] = TRUE;
                        Visit(w);
                        EnQueue(Q, w);
                    }
            }
        }
}

性能分析（与 DFS 相同）

连通性

通过遍历，可以判断图的连通性
- 无向图
  - 若连通，从任意一个顶点出发，只需一次遍历就能访问到途中所有顶点
  - 若非连通，从某一顶点出发，一次遍历只能访问到该顶点所在连通分量的所有顶点
- 有向图
  - 若初始点到图中所有顶点都有路径，则能够访问到图中所有的顶点；否则不能。

最小生成树

普里姆（Prim）算法

流程简述
- 初始化：向空树 $T=(V_T,E_T)$ 中添加图 $G=(V,E)$ 的任一顶点 $u_0$ ，使 $V_T = \{u_0\}$ ， $E_T=\varnothing$
- 循环（重复下列操作至 $V_T=V$）：从图 $G$ 中选择满足 $\{(u,v)|u\in V_T, v\in V-V_T\}$ 且具有最小权值的边 $(u,v)$ ，并置 $V_T=V_T\cup \{v\}$ ， $E_T=E_T\cup \{(u,v)\}$

void Prim(G, T)
{
    T = 空集;                 // 初始化空树
    U = {w};                 // 添加任一顶点 w
    while((V-U) != 空集)      // 若树中不含全部顶点
    {
        设 (u,v) 是使 u∈U 与 v∈(V-U)，且权值最小的边;
        T = T∪{(u, v)};     // 边归入树
        U = U∪{v};          // 顶点归入树
    }
}

性能分析
- 时间复杂度：$O( |V| ^2)$
适用于求解边稠密的图的最小生成树

克鲁斯卡尔（Kruskal）算法

流程简述
- 初始化： $V_T = V $ ， $E_T=\varnothing$ 。即每个顶点构成一颗独立的树， $T$ 此时是一个仅含 $|V|$ 个顶点的森林
- 循环（重复下列操作至 $T$ 是一棵树）：按 $G$ 的边权值递增的顺序依次从 $E-E_T$ 中选择一条边，若这条边加入 $T$ 后不构成回路，则将其加入 $E_T$ ，否则舍弃，直到 $E_T$ 中含有 $n-1$ 条边

void Kruskal(V, T)
{
    T = V;                  // 初始化树 T，仅含顶点
    numS = n;               // 连通分量数
    while(numS > 1)         // 若连通分量数大于 1
    {
        从 E 中取出权值最小的边 (v,u);
        if(v 和 u 属于 T 中不同的连通分量)
        {
            T = T∪{(v, u)}; // 边归入树
            numS--;          // 连通分量减1
        }
    }
}

性能分析
- 时间复杂度：$O(|E|log|E|)$
适用于求解边稀疏而顶点较多的图的最小生成树

拓扑排序

流程简述
- 在有向图中选择一个没有前驱的顶点并输出
- 从图中删除该顶点和以它为尾的弧
- 重复以上两步，直至全部顶点均以输出

Status TopologicalSort(ALGraph G)
{   /* 有向图G采用邻接表存储结构。若G无回路,则输出G的顶点的一个拓扑序列并返回OK, */
    /* 否则返回ERROR。算法7.12 */
    int i,k,count,indegree[MAX_VERTEX_NUM];
    SqStack S;
    ArcNode *p;
    FindInDegree(G,indegree); /* 对各顶点求入度indegree[0..vernum-1] */
    InitStack(&S); /* 初始化栈 */
    for(i=0;i<G.vexnum;++i) /* 建零入度顶点栈S */
        if(!indegree[i])
            Push(&S,i); /* 入度为0者进栈 */
    count=0; /* 对输出顶点计数 */
    while(!StackEmpty(S))
    { /* 栈不空 */
        Pop(&S,&i);
        printf("%s ",G.vertices[i].data); /* 输出i号顶点并计数 */
        ++count;
        for(p=G.vertices[i].firstarc;p;p=p->nextarc)
        { /* 对i号顶点的每个邻接点的入度减1 */
            k=p->adjvex;
            if(!(--indegree[k])) /* 若入度减为0,则入栈 */
                Push(&S,k);
        }
    }
    if(count<G.vexnum)
    {
        printf("此有向图有回路\n");
        return ERROR;
    }
    else
    {
        printf("为一个拓扑序列。\n");
        return OK;
    }
}

性能分析
- 时间复杂度：$O(|V|+|E|)$

关键路径

Status TopologicalOrder(ALGraph G,SqStack *T)
{ /* 算法7.13  有向网G采用邻接表存储结构,求各顶点事件的最早发生时间ve */
    /* (全局变量)。T为拓扑序列顶点栈,S为零入度顶点栈。若G无回路,则用栈T */
    /* 返回G的一个拓扑序列,且函数值为OK,否则为ERROR */
    int j,k,count,indegree[MAX_VERTEX_NUM];
    SqStack S;
    ArcNode *p;
    FindInDegree(G,indegree);/*对各顶点求入度indegree[0..vernum-1] */
    InitStack(&S); /* 初始化栈 */
    for(j=0;j<G.vexnum;++j) /* 建零入度顶点栈S */
        if(!indegree[j])
            Push(&S,j); /* 入度为0者进栈 */
    InitStack(T); /* 初始化拓扑序列顶点栈 */
    count=0; /* 对输出顶点计数 */
    for(j=0;j<G.vexnum;++j) /* 初始化ve[]=0 (最小值) */
        ve[j]=0;
    while(!StackEmpty(S))
    { /* 栈不空 */
        Pop(&S,&j);
        Push(T,j); /* j号顶点入T栈并计数 */
        ++count;
        for(p=G.vertices[j].firstarc;p;p=p->nextarc)
        { /* 对j号顶点的每个邻接点的入度减1 */
            k=p->adjvex;
            if(--indegree[k]==0) /* 若入度减为0,则入栈 */
                Push(&S,k);
            if(ve[j]+*(p->info)>ve[k])
                ve[k]=ve[j]+*(p->info);
        }
    }
    if(count<G.vexnum)
    {
        printf("此有向网有回路\n");
        return ERROR;
    }
    else
        return OK;
}

Status CriticalPath(ALGraph G)
{ /* 算法7.14 G为有向网,输出G的各项关键活动 */
    int vl[MAX_VERTEX_NUM];
    SqStack T;
    int i,j,k,ee,el;
    ArcNode *p;
    char dut,tag;
    if(!TopologicalOrder(G,&T)) /* 产生有向环 */
        return ERROR;
    j=ve[0];
    for(i=1;i<G.vexnum;i++) /* j=Max(ve[]) 完成点的值 */
        if(ve[i]>j)
            j=ve[i];
    for(i=0;i<G.vexnum;i++) /* 初始化顶点事件的最迟发生时间(最大值) */
        vl[i]=j; /* 完成点的最早发生时间 */
    while(!StackEmpty(T)) /* 按拓扑逆序求各顶点的vl值 */
        for(Pop(&T,&j),p=G.vertices[j].firstarc;p;p=p->nextarc)
        {
            k=p->adjvex;
            dut=*(p->info); /* dut<j,k> */
            if(vl[k]-dut<vl[j])
                vl[j]=vl[k]-dut;
        }
    printf(" j  k  dut  ee  el  tag\n");
    for(j=0;j<G.vexnum;++j) /* 求ee,el和关键活动 */
        for(p=G.vertices[j].firstarc;p;p=p->nextarc)
        {
            k=p->adjvex;
            dut=*(p->info);
            ee=ve[j];
            el=vl[k]-dut;
            tag=(ee==el)?'*':' ';
            printf("%2d %2d %3d %3d %3d    %c\n",j,k,dut,ee,el,tag); /* 输出关键活动 */
        }
    printf("关键活动为:\n");
    for(j=0;j<G.vexnum;++j) /* 同上 */
        for(p=G.vertices[j].firstarc;p;p=p->nextarc)
        {
            k=p->adjvex;
            dut=*(p->info);
            if(ve[j]==vl[k]-dut)
                printf("%s→%s\n",G.vertices[j].data,G.vertices[k].data); /* 输出关键活动 */
        }
    return OK;
}

性能分析
- 时间复杂度：$O(|V|+|E|)$

最短路径

迪杰斯特拉算法

void ShortestPath_DIJ(MGraph G,int v0,PathMatrix *P,ShortPathTable *D)
{ /* 用Dijkstra算法求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度 */
    /* D[v]。若P[v][w]为TRUE,则w是从v0到v当前求得最短路径上的顶点。 */
    /* final[v]为TRUE当且仅当v∈S,即已经求得从v0到v的最短路径 算法7.15 */
    int v,w,i,j,min;
    Status final[MAX_VERTEX_NUM];
    for(v=0;v<G.vexnum;++v)
    {
        final[v]=FALSE;
        (*D)[v]=G.arcs[v0][v].adj;
        for(w=0;w<G.vexnum;++w)
            (*P)[v][w]=FALSE; /* 设空路径 */
        if((*D)[v]<INFINITY)
        {
            (*P)[v][v0]=TRUE;
            (*P)[v][v]=TRUE;
        }
    }
    (*D)[v0]=0;
    final[v0]=TRUE; /* 初始化,v0顶点属于S集 */
    for(i=1;i<G.vexnum;++i) /* 其余G.vexnum-1个顶点 */
    { /* 开始主循环,每次求得v0到某个v顶点的最短路径,并加v到S集 */
        min=INFINITY; /* 当前所知离v0顶点的最近距离 */
        for(w=0;w<G.vexnum;++w)
            if(!final[w]) /* w顶点在V-S中 */
                if((*D)[w]<min)
                {
                    v=w;
                    min=(*D)[w];
                } /* w顶点离v0顶点更近 */
        final[v]=TRUE; /* 离v0顶点最近的v加入S集 */
        for(w=0;w<G.vexnum;++w) /* 更新当前最短路径及距离 */
        {
            if(!final[w]&&min<INFINITY&&G.arcs[v][w].adj<INFINITY&&(min+G.arcs[v][w].adj<(*D)[w]))
            { /* 修改D[w]和P[w],w∈V-S */
                (*D)[w]=min+G.arcs[v][w].adj;
                for(j=0;j<G.vexnum;++j)
                    (*P)[w][j]=(*P)[v][j];
                (*P)[w][w]=TRUE;
            }
        }
    }
}

性能分析
- 时间复杂度：$O(|V|^2)$

### 弗洛伊德算法

void ShortestPath_FLOYD(MGraph G,PathMatrix *P,DistancMatrix *D)
{ /* 用Floyd算法求有向网G中各对顶点v和w之间的最短路径P[v][w]及其 */
    /* 带权长度D[v][w]。若P[v][w][u]为TRUE,则u是从v到w当前求得最短 */
    /* 路径上的顶点。算法7.16 */
    int u,v,w,i;
    for(v=0;v<G.vexnum;v++) /* 各对结点之间初始已知路径及距离 */
        for(w=0;w<G.vexnum;w++)
        {
            (*D)[v][w]=G.arcs[v][w].adj;
            for(u=0;u<G.vexnum;u++)
                (*P)[v][w][u]=FALSE;
            if((*D)[v][w]<INFINITY) /* 从v到w有直接路径 */
            {
                (*P)[v][w][v]=TRUE;
                (*P)[v][w][w]=TRUE;
            }
        }
    for(u=0;u<G.vexnum;u++)
        for(v=0;v<G.vexnum;v++)
            for(w=0;w<G.vexnum;w++)
                if((*D)[v][u]+(*D)[u][w]<(*D)[v][w]) /* 从v经u到w的一条路径更短 */
                {
                    (*D)[v][w]=(*D)[v][u]+(*D)[u][w];
                    for(i=0;i<G.vexnum;i++)
                        (*P)[v][w][i]=(*P)[v][u][i]||(*P)[u][w][i];
                }
}

性能分析
- 时间复杂度：$O(|V|^3)$

解题技巧小结及结论补充

图的应用相关算法手算流程小结

最小生成树

Prim 算法

集合定义
- $V_T$ ：最小生成树中间结果的点集（初始化，任取一点，或题设给出）；
- $V-V_T$ ：还未归入最小生成树的点集
循环（直到 $V_T = V$）
- $V_T$ 中取一点 $u$ ， $V-V_T$ 中取一点 $v$ ，使得 $(u,v)$ 权值最小。
- 将 $v$ 并入集合 $V_T$

Kruskal 算法

集合定义
- $V_T$ ：最小生成树的点集（初始化为 $V$ ，即包含所有图中的点）
- $E_T$ ：存储最小生成树生成过程中边的集合（初始化为 $\varnothing$）
循环（直至 $T$ 是一棵树）
- 按 $G$ 的边权值递增的顺序依次从 $E-E_T$ 中选择一条边，若这条边加入 $T$ 后不构成回路，则将其加入 $E_T$ ，否则舍弃，直到 $E_T$ 中含有 $n-1$ 条边

最短路径

Dijkstra 算法

利用表格法求解

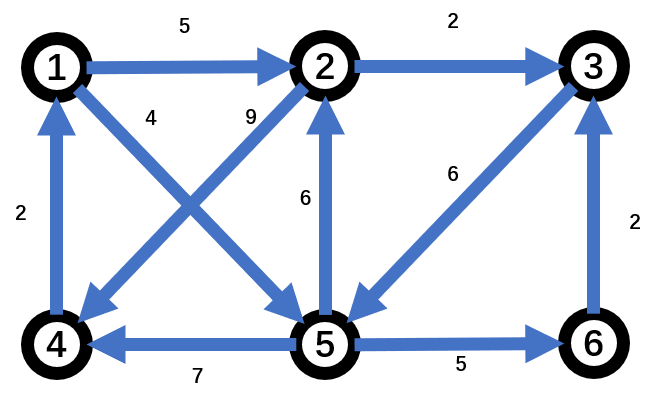
画下面的表格
- 起点直接能到达的结点在表格中的位置处填入，路径和对应长度。
- 不能直接到达的填正无穷。
- 将这一列的路径使得路径长度最短的结点（该路径此时的终点），并入集合 S 中（起点默认已经并入）
- 基于上一步得到的路径，看其终点有没有与其他点（这里的其他点 $\in V-S$）之间相连。有的话，计算这个新的路径长度，并与上一个（对应行的左边一个）比较：若更小，则更新；否则照抄。
- 由此得到新的一列，继续比较路径大小。然后，选择最小的，将对应的结点并入 S 。
- 以此类推，得到以下表格：

	i=1	i= 2	i=3	i=4	i=5
1（起点）
2	（1，2）、5	（1，2）、5（小）
3	$\infty$	$\infty$	（1，2，3）、7（小）
4	$\infty$	（1，5，4）、11	（1，5，4）、11	（1，5，4）、11	（1，5，4）、11
5	（1，5）、4（小）
6	$\infty$	（1，5，6）、9	（1，5，6）、9	（1，5，6）、9（小）
S	{1，5}	{1，5，2}	{1，5，2，3}	{1，5，2，3，6}	{1，5，2，3，6，4}

Floyd 算法

初始化 $dis^{(-1)}$ 为图的邻接矩阵
循环（邻接矩阵有 n 阶，外层就循环 n 次【从 0 到 n - 1】，主要是为了取将要加入以下路径点的点，设为 $V_{intermediate}$）
内部再套两个循环（主要是为了取任意两个点的组合，设这两个点为

\[ V_{source}和V_{end} \]

）比较 \[ (1)\ Weight(V_{source},V_{intermediate})+Weight(V_{intermediate}, V_{end}) \]

和 \[ (2)\ Weight(V_{source},V_{end}) \] 大小，若（1）式更小，则更新对应 $dis^{i}$ （i 代表循环变量【从 0 开始】）的

$V_{source}$所在行，

$V_{end}$所在列处的值

为（1）式子的结果。

拓扑排序

较简单，具体见上

关键路径

几个时间的计算
- 顶点相关
  - 事件 $v_k$ 最早发生的时间 $v_e(k)$
    - 从前往后算，计算从源点到当前点最长的路径长度。
    - 入度＞1 要注意，要取和最大
  - 事件 $v_k$ 最迟发生的时间$v_l(k)$
    - 从后往前算（通常是后一个结点的最迟时间，减去这两点之间的权值）
    - 出度＞1 要注意，要取差最小
- 弧相关
  - 活动 $a_i$ 最早开始时间 $e(i)$
    - 设 $a_i$ 夹在两个顶点 $v_k,v_j$ 之间，且 $v_k$ 在前，则$e(i) = v_e(k)$ （即前一个顶点最早发生时间）
  - 活动 $a_i$ 最迟开始时间 $l(i)$
    - 设 $a_i$ 夹在两个顶点 $v_k,v_j$ 之间，且 $v_k$ 在前，则$l(i) = v_l(k)-Weight(v_k,v_j)$ （即后一个顶点最迟发生时间【减去】两点之间的权值）

图的重要概念辨析及相关重要结论

重要概念辨析

无向完全图 VS 有向完全图

无向完全图：任意两个顶点都存在边
有向完全图：任意两个顶点都存在相反的两条弧

强连通图 VS 连通图

强连通图：（针对有向图）任意一对顶点都是强连通的（若从顶点 v 到 w 和 w 到v 都有路径，则这两个顶点是强连通的）
连通图：（针对无向图）任意两个顶点都是连通的（若从顶点 v 到 w 有路径，则这两个顶点是连通的）

强连通分量 VS 连通分量

强连通分量：（针对有向图）即为有向图中的极大强连通子图
连通分量：（针对无向图）即为无向图中的极大连通子图

重要结论

非连通图的判定：$|V| = n\ 且\ |E| <n-1$
无向图顶点的度:

\[ \sum^{n}_{i=1}TD(v_{i})=2|E| \]

有向图顶点的度:

\[ \sum^{n}_{i=1}ID(v_{i})=\sum^{n}_{i=1}OD(v_{i})= |E| \]

边数最少：对于连通无向图，即构成一棵树；对于强连通有向图，即构成一个有向环
一些极端情况可以考虑完全图、环等作为排除选项的反例。
图与树遍历关系
- 广度优先搜索相当于二叉树中的层序遍历
- 深度优先搜索相当于树中的先序遍历
广度优先搜索可用于解决无权（或等权）单源最短路径问题
遍历唯一性
- 邻接矩阵存储：唯一
- 邻接表存储：不唯一
有向图中的回路判定方法
- 拓扑排序
- 深度优先搜索：如果遍历过程中，将要访问的结点已在栈中，则有回路。
DFS入栈顺序拓扑有序
一个连通图的生成树是图的极小连通子图
最小生成树的性质
- 一般形状不唯一（当图中各边权值互不相等，最小生成树唯一）
- 权值和唯一
- （★★★）边数 = 顶点数 - 1
单源最短路径，使用 Dijkstra ；每对顶点的的最短路径，使用 Floyd
Dijkstra 不适用于带负权值；Floyd 不适用于包含带负权值的边组成回路
n 个顶点、e 条弧有向图采用邻接表存储，拓扑排序时间复杂度O(n+e)（排序过程中，先找入度为 0 的点，再删除，非嵌套！另一角度，拓扑排序即是最终删除所有顶点和边，有 n 个顶点，e 条边，故总时间复杂度为 O(n+e)）
若一有向图不能排成一个拓扑序列，则该图有环
要缩短工期，则所有关键路径上的点（每个关键路径上至少挑选一个进行时间压缩）都要同时减少（步骤：①找关键结点，得到其路径长度【设为 L】；②找所有路径长度为 L 的路径；③找到几个点，他们能覆盖到所有关键路径）
若用邻接矩阵存储有向图，矩阵中主对角线以下的元素均为 0 。则该图的拓扑排序存在，但不唯一（ 2012 统考）

参考资料

数据结构（C语言版）.严蔚敏等
2020年数据结构考研复习指导.王道论坛

CosmosNing的个人博客

数据结构复习笔记6-图

7．图

图的基本概念；图的存储表示：邻接矩阵、邻接表

基本概念

存储表示

邻接矩阵

邻接表

图的遍历与连通性

遍历

深度优先搜索

广度优先搜索

连通性

最小生成树

普里姆（Prim）算法

克鲁斯卡尔（Kruskal）算法

拓扑排序

关键路径

最短路径

迪杰斯特拉算法

### 弗洛伊德算法

解题技巧小结及结论补充

图的应用相关算法手算流程小结

最小生成树

Prim 算法

Kruskal 算法

最短路径

Dijkstra 算法

Floyd 算法

拓扑排序

关键路径

图的重要概念辨析及相关重要结论

重要概念辨析

无向完全图 VS 有向完全图

强连通图 VS 连通图

强连通分量 VS 连通分量

重要结论

参考资料