2.运算方法与运算部件
(★★)数制与编码
进位计数制及其相互转换
进位计数制
- r 进制数可表示为
- \(\sum_{i=n}^{-m}K_ir^i\)
- 其中 r 是基数,\(K_i\) 的取值可以是 0 , 1, ··· , r - 1共 r 个数码中的任意一个
相互转换
R 进制 -> 十进制
- 按权展开即可
十进制 -> R 进制
- 整数部分:除基取余,上右下左
- 小数部分:乘基取整,上左下右
八进制 <-> 二进制
- 1 位八进制对应 3 位 二进制
- 二进制转八进制,若位数不够,则整数部分高位补 0 ,小数部分低位补 0
十六进制 <-> 二进制
- 1 位八进制对应 4 位 二进制
- 二进制转十六进制,若位数不够,则整数部分高位补 0 ,小数部分低位补 0
真值和机器数
- 真值:带有 “+” 和 “-” 的数
- 机器数:用 “0” 和 “1” 代表数字符号的数,包括 原码、补码、反码等
BCD编码
- 用 4 位 二进制数来表示十进制中 0~9 这 10 个数码。(由于 2 的 4 次方 为 16 ,故有 6 个冗余状态)
- 8421码:每 4 位 对应 1 个十进制位。
- 相加修正
- 若对应位相加结果 <= 十进制的 9 ,则不需要修正
- 若大于,则要加 6 修正 ,并向高位进位
- 相加修正
字符与字符串
ASCII 码
- 7 位二进制表示
汉字
- 汉字编码包括输入编码、汉字内码、汉字字形码
- 区域码:两个字节表示一个汉字,每个字节 7 位
- \(国标码 = (区位码)_{16}+2020H\)
- \(汉字内码 = (国标码)_{16}+8080H\)
字符串的存放
- 大端:高位字节到低位字节依次存放
- 小端:低位字节到高位字节依次存放
- 注意:是以字节为单位存放,不是以位为单位存放
校验码
奇偶校验
- 奇校验: 1 的个数为奇数
- 偶校验: 1 的个数为偶数
海明校验



循环冗余(CRC)校验
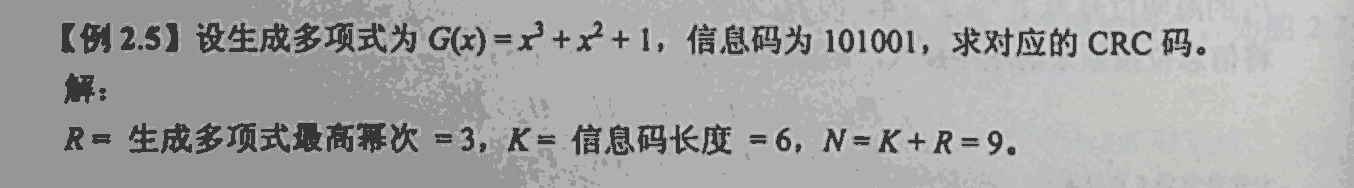


(★★★)定点数的表示、运算与运算部件
无符号数与有符号整数的表示
概述
- 无符号数:所有位为数值位
- 有符号数:第一位为符号位( 0 为 正,1 为负),剩余位为数值位
原码
- 最高位为符号位,剩余位为数值位,表示该数的绝对值
- 0 有两种表示
补码
- 原码到补码的转换
- 正数:不变
- 负数:符号位不变,数值位按位取反,末位加一
- 0 仅有一种表示
反码
- 原码到反码的转换
- 正数;不变
- 负数:符号位不变,数值位按位取反
- 0 有两种表示
移码
- 补码到移码的转换:补码的符号位取反,即得到对应的移码
- 0 仅有一种表示
补码定点数加减法运算
- 公式 \[ [A+B]_{补}=[A]_{补}+[B]_{补} \] \[ [A-B]_{补}=[A]_{补}+[-B]_{补} \]
- 注意:运算结果仍为补码,此步计算完后,要回化,转为机器数或者真值
定点数乘除运算
原码一位乘
- 步骤:
- 操作数取绝对值运算,结果符号位取操作数符号位的异或结果。
- 部分积长度同被乘数,取 n + 1 位(双符号位),初值为 0
- 从乘数的最低位开始判断
- 若最低位为 1,部分积加上 | x | ,再右移一位
- 若最低位为 0,部分积加上 0 ,再右移一位
- 重复 3
注:最后结果要加上符号位:符号位 1 异或 0 = 1 ,最终得 x 乘 y = -0.10001111
补码一位乘
- 步骤:
- 符号位参与运算,运算的数均以补码表示
- 被乘数一般取双符号位,部分积取双符号位,初值为 0 ,乘数可取单符号位
- 乘数末位增设附加位 \(y_{n+1}\) ,且初值为 0
- 对应下面的表格,进行相关操作
- 移位按补码右移规则进行
- 循环上述操作
- Booth 算法的移位规则
| \(y_n\)(高位) | \(y_{n+1}\)(低位) | 操作 |
|---|---|---|
| 0 | 1 | 部分积右移一位 |
| 0 | 1 | 部分积加\([X]_{补}\) ,右移一位 |
| 1 | 0 | 部分积加\([-X]_{补}\) ,右移一位 |
| 1 | 1 | 部分积右移一位 |

原码除法(不恢复余数法)
- 步骤:
- 符号位不参与运算,结果符号位为操作数符号位两者的异或
- 用被除数减去乘数
- 若余数为正,商上 1 ,左移一位,再减去除数
- 若余数为负,商上 0 ,左移一位,再加上除数
- 当最后一步,余数为负(上商 0 ),需要加上除数,得到正确的余数

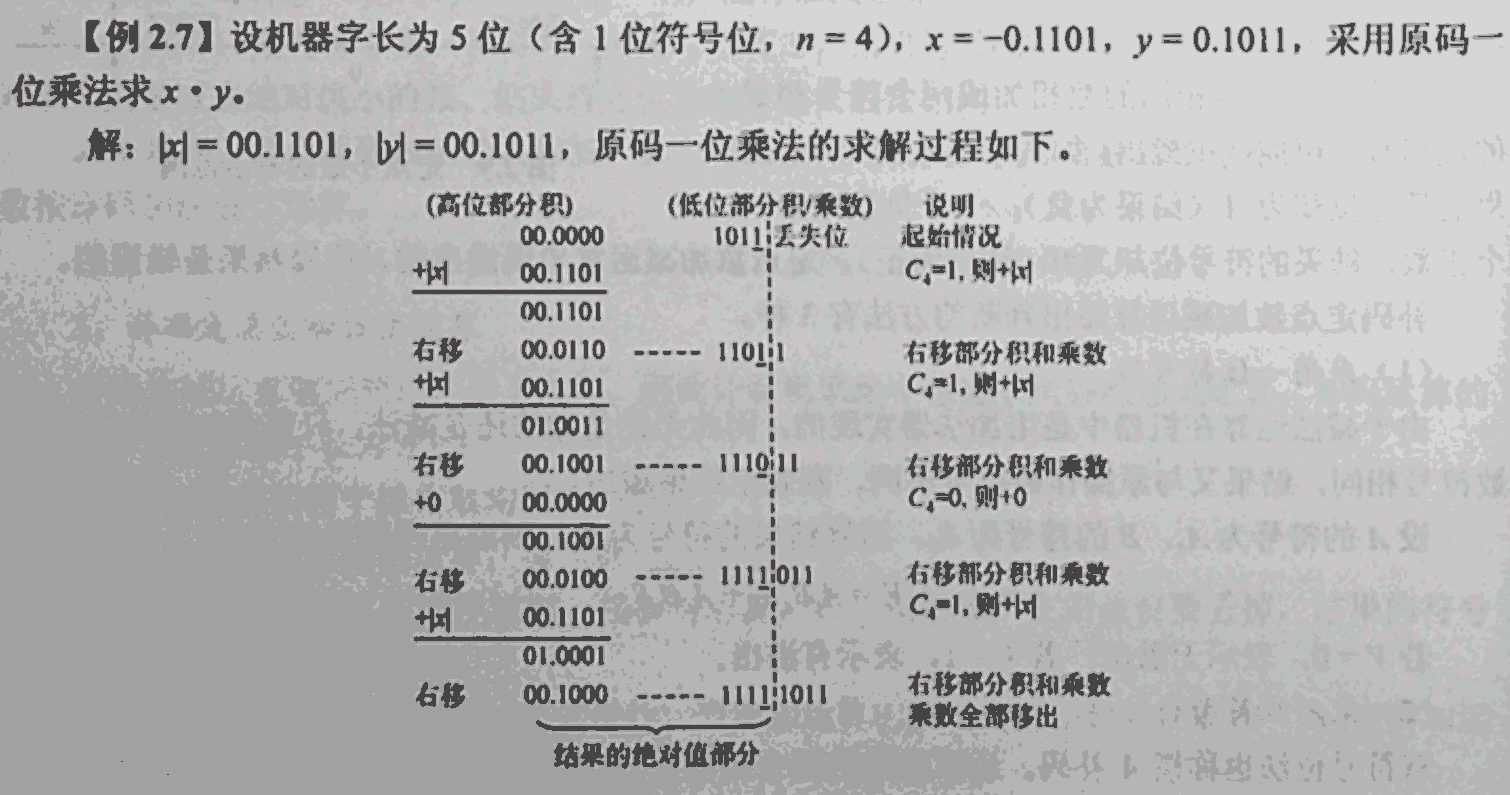
补码除法(加减交替法)
- 步骤:
- 符号位参与运算,运算的数均以补码表示
- 若被除数与除数同号,则被除数减去除数;若被除数与除数异号,则被除数加上除数(同号相减,异号相加)
- 若余数与除数同号,则商上 1 ,左移一位,减去除数;若余数与除数异号,则商上 0 ,左移一位,加上除数(同号商 1 左移减,异号商 0 左移加)
- 重复 3
溢出概念和判别方法
概念
- 运算结果超出了表示范围
判别方法
一位符号位
- 原操作数符号相同,结果符号与原操作不同,结果溢出
双符号位
- 运算结果双符号位相同,表示未溢出
- 运算结果双符号位不同,表示溢出,符号位最高位决定正负
移位运算
算术移位
- 针对有符号数,移位过程中符号位不变
- (★★★★)移位后填补空位原则如下表
| 码制 | 添补代码 | |
|---|---|---|
| 正数 | 原码、补码、反码 | 0 |
| 负数 | 原码 | 0 |
| 补码 | 左移添 0 | |
| 右移添 1 | ||
| 反码 | 1 |
逻辑移位
- 针对无符号数(或者说把该机器数当成无符号数)
- 移位规则
- 左移和右移,空位都添 0
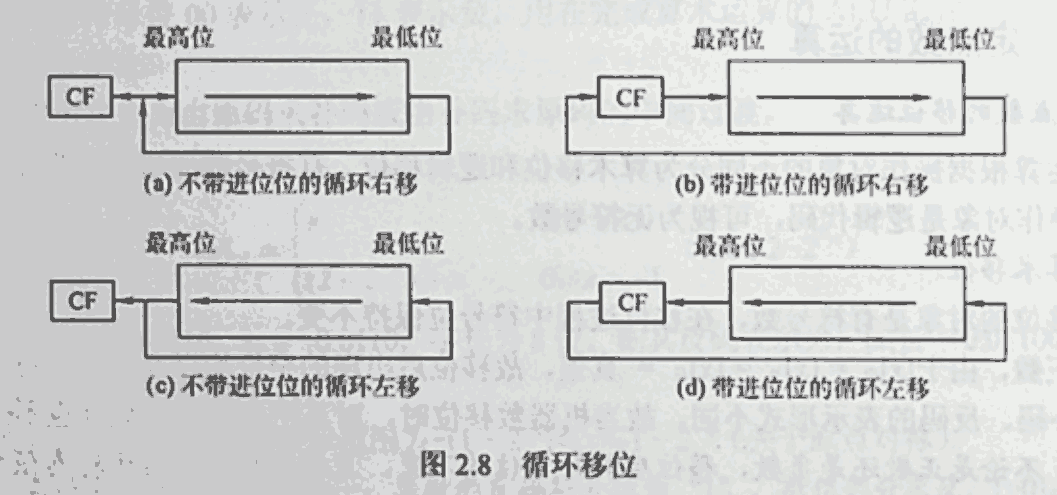
循环移位
(★★)浮点数的表示与运算
浮点数的表示
- \(N=r^E\times M\)
- 其中,r 为阶码的底(隐含,在计算机中 r = 2),E 为阶码,M 为尾数
IEEE754标准
- 统一数据格式如下表
| \(m_s\) | \(E\) | \(M\) |
|---|---|---|
| 数符 | 阶码(移码表示) | 尾数(原码表示) |
- 不同类型浮点数数位安排
| 类型 | 数符 | 阶码 | 尾数数值 | 总位数 | 偏置值 |
|---|---|---|---|---|---|
| 短浮点数(float) | 1 | 8 | 23 | 32 | 127(7FH) |
| 长浮点数(double) | 1 | 11 | 52 | 64 | 1023(3FFH) |
- 注
- 由于规格化后,尾数最高位总为 1 ,可将此位隐含,故尾数实际可多存一位(还原此浮点数时,需要补上最高位的 1)
- 以短浮点数为例
- 偏置值为 127 (而非 128 ),因为要用全1表示无穷大
- 阶码范围为 1~254,因为全0表示非规格化数
浮点数的加减运算
- 步骤
- 对阶
- 小阶向大阶看齐:小阶右移,阶增加,直至阶码相等
- 尾数求和
- 规格化(详见下一个标题)
- 舍入
- 0 舍 1 入
- 尾数右移
- 低位丢弃了 0 ,则舍去
- 低位丢弃了 1 ,则尾数加一(可能导致溢出,需右规处理)
- 尾数右移
- 恒置 1
- 尾数右移,低位恒置 1
- 0 舍 1 入
- 溢出判断
- 双符号位补码:双符号位相同,未溢出;双符号位不同,溢出。溢出情况又分为
- 双符号位为 10,下溢
- 双符号位为 01,上溢
- 双符号位补码:双符号位相同,未溢出;双符号位不同,溢出。溢出情况又分为
- 对阶
浮点数规格化
- 规格化后
- 原码:最高数值位总为 1
- 补码:符号位和最高数值位不同
- 根据这个性质,可判断浮点数中的尾数是否是规格化数
- 非规格化尾数的规格化操作
- 左规
- 左移一位,阶码减一
- 右规
- 右移一位,阶码加一
- 左规
(★)ALU的功能与结构
补码加减运算器的实现
(详见教材)
典型指令完成设计与实现
(详见教材)
(★★)掌握不同层次程序员看到的运算
高级语言以C语言为例
(详见教材)
ISA层面则以MIPS32为例
(详见教材)
解题技巧及重要结论
- BCD 码表示的数相加减,可以先将两数转换为十进制(每 4 位二进制位看成 1 位十进制位),十进制相加减,在将十进制结果转换为 BCD 码表示。
- 判断 8421 BCD 码的合法性:检查是否出现 1010~1111 范围内的二进制数,若有,则非法。
- 海明校验码能纠一位错应该满足 \(2^k\ge n+k +1\) ,其中 n 为数据位数,k 为校验位数
- 一种判运算结果溢出的技巧:全部转换成十进制进行对应计算,在依据数据位数所确定的数据表示范围,来判断结果是否溢出。
- 补码表示时,若符号位相同,则数值位越大码越大
参考资料
- 计算机组成与系统结构.袁春风等
- 2020年计算机组成原理考研复习指导.王道论坛