KAT: Keywords-to-SPARQL Translation Over RDF Graphs 阅读笔记

Highlights

• Two-Facet Indexing：这篇文章的关键词索引和图索引看上去比较简单，而且十分高效。
• Context Aware Ranking：充分利用关键词的上下文信息和 RDF 模式的信息，构建了一种十分有效的排序方法。

What？

Problem

将关键词查询高效的转换为 SPARQL 查询（keyword-to-SPARQL）

Contributions

本文主要构建了一个关键词查询系统 KAT ，它能够将关键词查询转换为 SPARQL 查询。与现存方法不同的是，它考虑了上下文（context）信息和模式（schema）信息。主要的贡献如下：

1. 提出了一种新颖的关键词到 SPARQL 转换（keywords-to-SPARQL）方法（叫做 KAT）。
2. 构建了两个索引。一个为关键词索引（keyword index），另一个为图索引（graph index）。
3. 实验表明了 KAT 的有效性和高效性。

Why？

Necessity for a Keyword Query System in RDF Data

• RDF 提供了一种灵活的方式表示知识
• SPARQL 是 RDF 的结构化查询语言。但是对于普通用户，尤其是不了解 RDF 内在模式（schema）或者是 SPARQL 语法的用户，使用 SPARQL 查询 RDF 数据将会极度困难。
• Keyword-to-SPARQL 通过自动地将关键词转换为 SPARQL 查询语句，使得用户可以更加简单地探索 RDF 数据。

Disadvantages of Existing Approaches

现存的解决方案无法有效并且高效地返回关键词查询的结果，主要原因如下：

• 没有考虑输入关键词的上下文信息
• 没有利用 RDF 图的模式信息（例如与某个关键词相关的 RDF 类）

Advantages of Proposed Method

• KAT 利用了关键字之间的上下文关系，提高了查询结果的相关性。
• 含有 RDF 类（class）信息的关键词索引（keyword index）将会解决关键词语义的模糊性问题（disambiguation），而图索引（graph index）将会加速图的探索过程（graph exploration）。
• 实验表明 KAT 处理更快，并且结果质量更好

How？

Keyword-to-SPARQL 方法的关键是在 RDF 数据中找到一个子图，这个子图包含输入的关键词并且满足用户的需求。

Overview

Overview of KAT. Source: "KAT: Keywords-to-SPARQL Translation Over RDF Graphs"

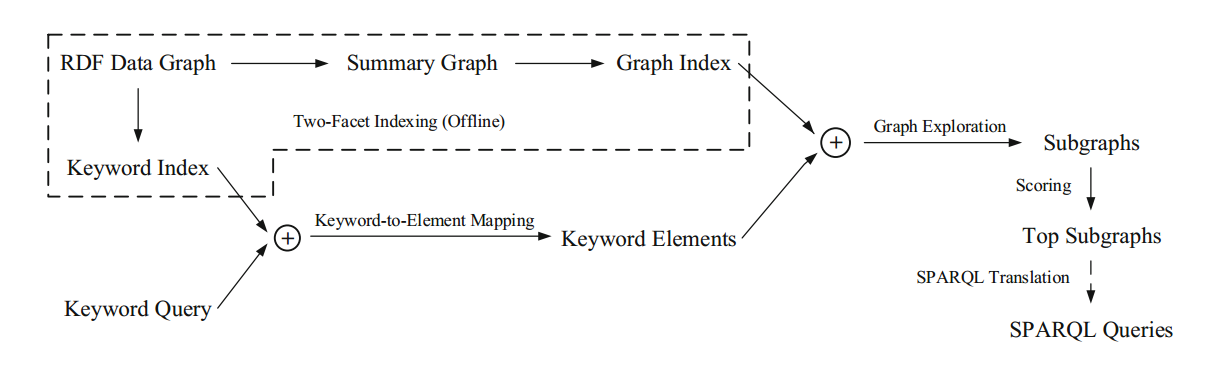
• 离线创建索引（Offline Two-Facet Indexing）：在离线处理流程中，系统将会创建两个索引，包括关键词索引和图索引。
• 创建关键词-元素映射（Keyword-to-Element Mapping）：当用户提交了一个关键词查询任务后，KAT 通过离线生成的关键词索引，将关键词映射到与之相关的顶点和边（这些顶点和边被称为 keyword elements）。
• 图探索（Graph Exploration）：然后，基于图索引进行图探索阶段，以找到含有关键词的子图。
• 排序（Ranking）：使用考虑上下文关系的评价方法，将子图从大到小排序。
• 翻译（Translation）：将排序前几名的子图翻译成 SPARQL 查询语句。

Two-Facet Indexing

Keyword Indexing

功能

将关键词映射到与之相关的元素。

现存方案的不足

现有方案中，关键词索引仅仅是一个简单的倒排索引（inverted index）。因此，在构建映射关系时，所有包含关键词的元素都被当作候选结果，这其中包括大量的无用元素。为什么会这样呢？这是由于自然语言关键词的二义性（ambiguity）导致的。例如，用户输入这样一个查询，{person, movie, lila} 。其查询意图为，找到在 “Lila Says” 中演出的演员。但是 “lila” 却是一个模棱两可的关键词，她可能是一个人名，也可能是一张专辑名，甚至是一个地铁名。

解决方案

为了减少关键词的二义性，这篇文章提出了一种混合索引，作为关键词索引。这个索引包含了 RDF 数据中各个术语（terms）的类别信息。其具体结构如下图所示：

Hybird Index. Source: "KAT: Keywords-to-SPARQL Translation Over RDF Graphs"

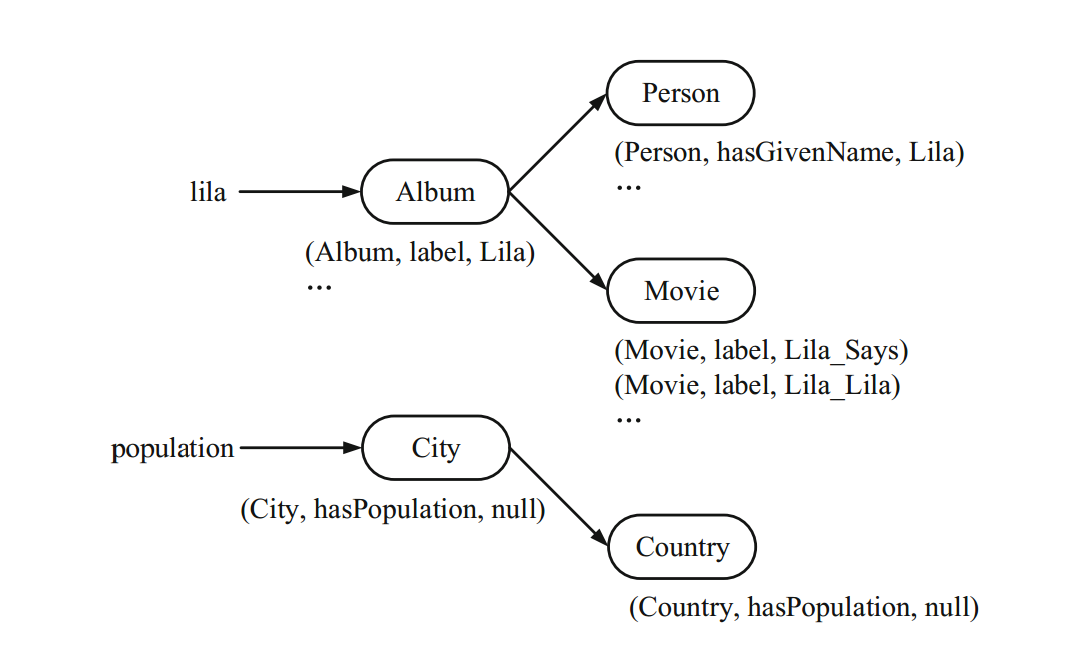
• 每一个术语（term）都指向一个由与之相关的所有可能的 RDF 类构成的 B 树。
• 包含术语的元素用 \((v_C,\ l_A,\ v_L)\) 表示，并且赋给 B 树上的对应结点，其中 \(v_C\in V_C,\ l_A\in L_A,\ v_L\in V_L\) 。
  • \(V_C\) 表示 RDF 图中的类顶点（class vertices）集合。
  • \(L_A\) 表示 RDF 图中的实体-字面量边标签（entity-literal edge labels）集合。
  • \(V_L\) 表示 RDF 图中的字面量顶点（literal vertices）集合。

此外，设关键词 \(w\) 的关键词映射为 \(f:(w,C)\rightarrow K\) ，其中 \(C\) 为关键词 \(w\) 可能对应的 RDF 类别（class）集合，\(K\) 是关键词元素集合。特别的，集合 \(C\) 由以下类（class）组成：

• 无二义性关键词中提及的类（class）（例如 person 、movie）。
• 在 summary graph 中能在 n 跳之内到达上述类的类。

预期效果

这样，关键词就被映射到一个较小的并且高质量的关键词元素的集合上了。

Graph Indexing

功能

为了更加高效地在图上探索。

方案

捕捉实体类别中的关系形成一个较小的 summary graph，并将其当作图索引。一个例子如下图所示：

Summary graph. Source: "KAT: Keywords-to-SPARQL Translation Over RDF Graphs"

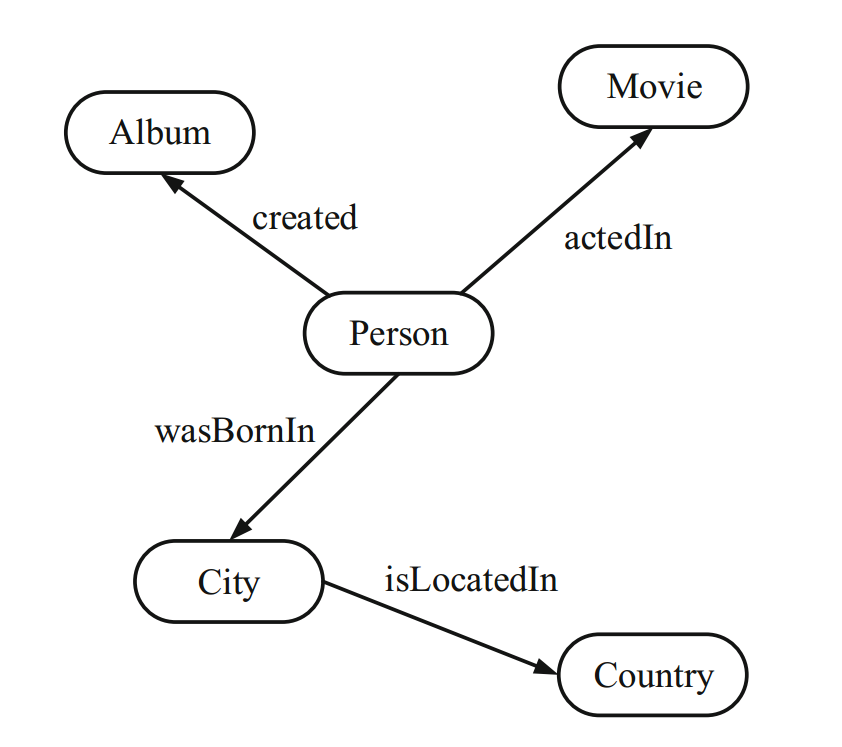
图探索基本过程

进行图探索常用的方法是后向搜索算法（backward search algorithm）。它在图索引上搜索符合条件的子图。该算法从关键词元素开始，然后沿着边进行迭代遍历，直到找到所有的连接点（connecting vertices）。一个例子如下图所示：

Subgraphs. Source: "KAT: Keywords-to-SPARQL Translation Over RDF Graphs"

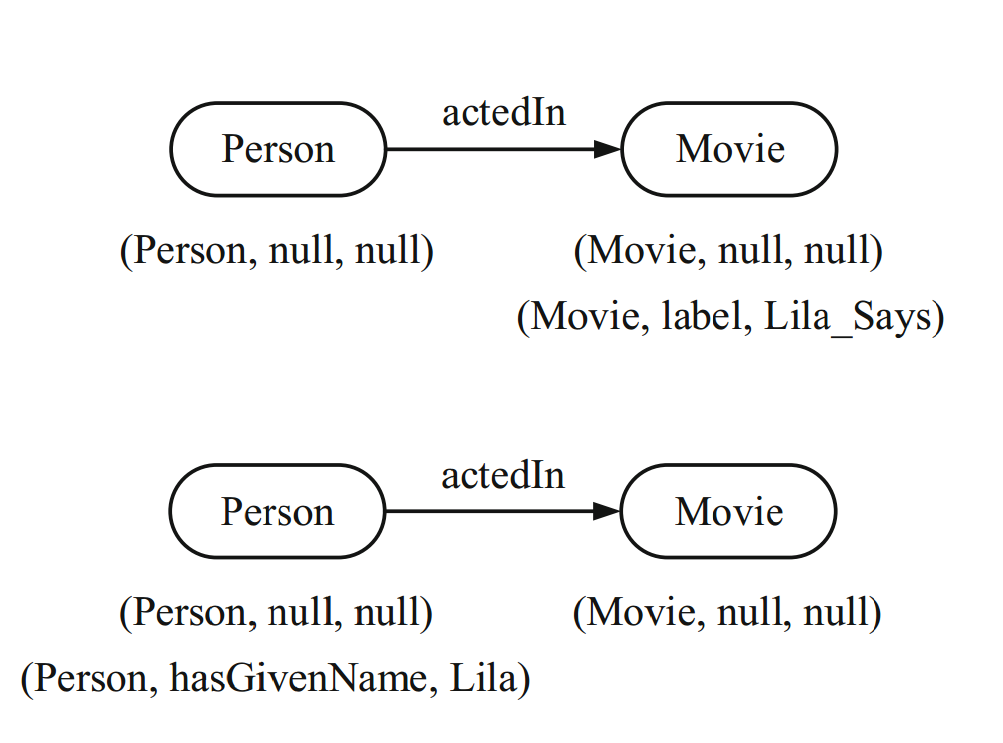
Context Aware Ranking

现有标准方法及其不足

现有方法基于子图的结构。具体来说，较小的子图往往是正确的答案。但是最小的子图并不一定满足用户的查询需求。

Context Aware 方案

为了克服这个缺陷，这篇文章提出了一种利用上下文信息的排名方法。通过这种方法可以计算子图和用户查找意图的相关性。具体的，该方法考虑了三种上下文信息：

• the relevance of a keyword element \((v_C,\ l_A,\ v_L)\) referring to a literal vertex increases if there is a keyword referring to a class semantically similar to \(v_C\) .
• the relevance of a keyword element \((v_C,\ l_A,\ null)\) referring to an entity-literal edge increases if there is a keyword referring to a class semantically similar to \(v_C\) .
• the relevance of a keyword element \((v_C,\ l_A,\ v_L)\) referring to a literal vertex increases if there is a keyword referring to an entity-literal edge \(l_A\) whose related class is semantically similar to \(v_C\) .

关键词元素打分算法

下图算法 1 描述了关键词元素打分的流程：

Algorithm 1. Source: "KAT: Keywords-to-SPARQL Translation Over RDF Graphs"

每个元素的分数都初始化为 0 ，并且基于上述三条规则递增。第 3 - 7 行遵循了第 1、2 条规则，第 8 - 12 行遵循了第 3 条规则。下式给出了计算 \(c_1\) 类和 \(c_2\) 类的 semantic similarity 的方法： \[ sim(c_1,\ c_2)=\frac{|S(c_1,\ O)\ \cap S(c_2,\ O)|}{|S(c_1,\ O)\ \cup S(c_2,\ O)|}\tag{1} \] 其中，\(S(c,\ O)\) 是指在 ontology \(O\) 中 \(c\) 的父类集合。

为什么这样计算类之间的 semantic similarity？

• 这是因为，如果两个类拥有更多相同的父类，那么这两个类往往是相似的。

• 式（1）中分子表示两个类的父类的交集的元素个数（也就是两者共有的父类个数），分母表示两个类的父类的并集的元素个数（也就是两者一共有多少不重复的父类）。

• 当分子越大，分母越小时，两者的 semantic similarity 就越大，这与上述原因是一致的。

给出两个关键词元素 \(k_1\) 和 \(k_2\) ，依据 \(k_1\) ，\(k_2\) 的相关度增量（relevance increment）可由下式得到： \[ rel(k_1,\ k_2) = \frac{sim(k_1.v_C,\ k_2.v_C)}{|pos(k_1) - pos(k_2)|}\tag{2} \] 其中 \(pos(k)\) 表示与 \(k\) 对应的关键词在关键词查询序列中的位置。

\(rel(k_1, k_2)\) 的简要分析

• 式（2）分子表示关键词元素的类别之间的相似度，分母表示两个关键词元素所对应的关键词在关键词查询序列中的距离。

• 相似度越高，关键词距离越短，相应的 \(rel\) 就越大。这个公式就巧妙地利用了 graph schema 和 关键词 的 context。

后续计算流程

• 子图分数的计算：将与子图相关的关键词元素的分数相加，并且除以子图中边的个数。即 \[ Score_{subgraph} = \frac{\sum{Score_{relvant-keyword-elements}}}{|E_{relevant-in-subgraph}|} \]

• 排序

• 翻译

How much？

• 由于 KAT 减少了关键词的模糊性，并且能够找到高度相关的子图，所以 KAT 的效果相较于传统方法更好。

• 虽然混合索引的空间占用更大，生成索引时间更长，但是却能够更快、更好地返回关键词查询结果。

What Then？

• 挖掘更多关键词中的模式信息（semantical information），来改进此方法。
• 可能存在某些方缩短图探索阶段的时间。

Problems to Solve

阅读这篇文章产生了以下问题，需要未来花时间解决：

• 倒排索引是什么？？
• B 树是什么，怎么创建？
• 怎样构建 Summary Graph ？？算法流程？？
• top graph -> SPARQL Query ？？ 具体怎么处理？
• 理解 backward search algorithm ：阅读更多文献 [1] ¹， [2] ²， [3] ³
• 怎么理解文中提出了三种上下文信息规则？

---

1. He, H., Wang, H., Yang, J., Yu, P.S.: BLINKS: ranked keyword searches on graphs. In: Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, pp. 305–316. ACM (2007)↩︎

2. Le, W., Li, F., Kementsietsidis, A., Duan, S.: Scalable keyword search on large RDF data. IEEE Trans. Knowl. Data Eng. 26(11), 2774–2788 (2014)↩︎

3. Tran, T., Wang, H., Rudolph, S., Cimiano, P.: Top-k exploration of query candidates for efficient keyword search on graph-shaped (RDF) data. In: 2009 IEEE 25th International Conference on Data Engineering, ICDE 2009, pp. 405–416. IEEE (2009)↩︎