Highlights
- Static Hub Labelings
- Dynamic Hub Labelings
What?
Problem
一种常见的图数据上的关键词查询的方法是,将每一个关键词与图上的一个顶点匹配,并且从中抽取出包含这些匹配顶点的最小权重的树(这种树被称为 minimum-weight Steiner trees)。更规范地说,给定一个有权边的数据图和一个关键词查询,首先对于每一个关键词,在图中找到与之匹配的所有顶点,形成一个匹配集;然后,在图中找到一个扩展匹配集的树,该树对于每一个匹配集,至少包含其中的一个顶点,并且总边权重最小。这个优化问题叫做 group Steiner tree (GST) problem 。
数据图中的边也可以被关键词匹配。我们可以通过 graph subdivision 将边匹配转换为点匹配,之后使用点匹配的方式处理该匹配就行了。
Contributions
- 设计了一个质量有保证的近似算法,能够在毫秒级内,从百万级大小的知识图谱中返回不错的结果。
- 设计了动态、静态 HL,提高了总体的效率。
Why?
知识图谱越来越大,现存的算法太慢了。
How?
Problem Formulation
- 知识图谱(KG):规范的,知识图谱是一个简单的无向图
\(G=<V,E>\) ,其中 \(V\) 是包含 \(n\)
个顶点的有限集合,用来指代实体(entity),而 \(E\subseteq V\times V\)
是顶点无序对的有限集合,作为图的无向边,用来代表实体之间的关系(relation)。
- 边权重:定义一个权重函数 \(\textrm{wt}:E\mapsto \mathbb{R}^{0+}\) (小权重表示重要性大)。
- 图中术语
- \(\textrm{len}(p)\) :对于一条路径 \(p\) ,它的长度是路径中所有边的权重之和。
- \(\textrm{dist}(u,v)\) :在图 \(G\) 中,连接 \(u\) 、\(v\) 的最短路径的长度。如果不存在,那么为 \(\infty\) 。
- 关键词映射:定义一个获取函数 \(\textrm{hits}:\mathbb{K}\mapsto 2^V\) ,它将关键词映射到顶点集 \(V\) 的子集。
- 关键词查询:一个关键词查询 \(Q\subseteq \mathbb{K}\)
是一个关键词的有限集合。
- 给定一个含有 \(g\) 个关键词的查询 \(Q=\{k_1,k_2,\dots,\ k_g\}\) ,将 \(\textrm{hits}(k_i)\) 简记为 \(K_i\) (\(1\le i\le g\)),并称之为关键词顶点。
- 给定一个图 \(G=<V,E>\) ,在
\(G\) 上关于 \(Q\) 的结果是一个 group Steiner tree
(GST) ,记作 \(T=<V_T,E_T>\)
,满足以下条件
- \(V_T\subseteq V,E_T\subseteq E\) ,并且 \(T\) 是一棵树;
- \(V_T\) 包含来自每一个 \(K_i\) (\(1\le i\le g\))中的至少一个顶点,也就是 \(V_T\cap K_i \ne \emptyset\) ;
- 树的权重(定义为 \(\textrm{WT}(T)=\sum_{e\in E_T}\textrm{wt}(e)\))最小
Overview of Two Algorithm
第一个算法 KeyKG 为每一个关键词选取匹配的顶点,并且找到对应的树。对于 \(g\) 个关键词,KeyKG 是一个 \((g-1)\) - 近似算法,也就是说,一个 GST 的边权值的总和至多是最小权重的 \((g-1)\) 倍。获得这样的近似效果要归功于匹配顶点集的选择和利用最短路径树的构造。为了更高效的在线计算距离和最短路径,该文章设计了一个 HL ,这个 HL 使用了一种全新的基于 betweenness centrality 的启发式方法改善了现存的 pruned landmark labeling 。传统的,这种 HL 是静态的,因为它是离线生成的,并且对查询是不变的。在巨大的知识图谱中, 使用静态 HL 的 KeyKG 算法至少比目前先进的算法快一个数量级,并且所得结果的质量也较高。
第二个算法 KeyKG+ 通过使用一种新颖的 HL 扩展了 KeyKG 算法。这里所提出的 HL 是动态的,因为它是在处理一个具体的查询时,通过倒排和聚集某些查询相关的静态标签,而动态生成的。它减少了 KeyKG 算法中的重复操作(这些重复操作是指使用传统静态 HL 计算顶点集的距离)。尽管在线生成会花费额外的时间,使用动态 HL 为总体效率带来了几个数量级的提高。
KeyKG With Static HL
Algorithm KeyKG
Algorithm Explained
如下图算法 1 所示,KeyKG 在知识图谱中找到一个 GST ,这个 GST 是由 \(g\) 个关键词集合扩展而来。简而言之, KeyKG 首先贪婪地选择一组相互靠近的一组关键词顶点集合(记作 \(U_x\)),这组关键词顶点集合包含了来自每一个 \(K_i\) (\(1\le i\le g\))中的一个顶点(Line 1 - 8)。然后,KeyKG 贪婪地找到一个由 \(U_x\) 扩展而来的 GST (记作 \(T_{u_{min}}\)),这个过程是通过迭代地扩展最短路径而得到的(Line 9 - 18)。

具体的,对于每一个 \(v_1 \in K_1\) (Line 1),KeyKG 从每一个 \(K_i\) 找到一个顶点 \(v_i\) ,它距离 \(v_1\) 的距离最短(Line 2 - 4)。令 \(U_{v_1}\) 为所有这样的顶点 \(v_i\) (包括 \(v_1\))的的集合,并且令 \(W_{v_1}\) 为它们到 \(v_1\) 的距离之和(Line 5 - 6)。令 \(x\in K_1\) 为 \(K_1\) 中 \(W_{v_1}\) 最小的顶点(Line 8)。
扩展 \(U_x\) 所得到的 GST 可能有较小的权重
- 因为 \(U_x\) 包含了来自每一个 \(K_i\) (\(1\le i\le g\))中的一个顶点,并且这些顶点相对而言十分接近,所以扩展 \(U_x\) 所得到的 GST 可能有较小的权重。
算法 1 剩下的部分以每一个 \(u\in U_x\) 构造一个 GST \(T_u\) ,并且从这 \(|U_x|\) 棵 GST 中找出权重最小的那一个。具体的,每一棵 \(T_u\) 被初始化为只含有一个单一的顶点 \(u\) (Line 9 - 10)。然后,不断迭代直至 \(T_u\) 扩展了 \(U_x\) 中的所有顶点(Line 11):从 \(T_u\) 中选取一个点 \(s_{\textrm{min}}\) ,从 \(U_x-T_u\) 中选一个点 \(t_{\textrm{min}}\) ,它们之间的距离最短(Line 12)。接着,找到 \(s_{\textrm{min}}\) 和 \(t_{\textrm{min}}\) 之间的最短路径,并将路径上的顶点和边加入 \(T_u\) (Line 13 -14)。令 \(u_{\textrm{min}}\in U_x\) 表示一个顶点,满足它所对应的 \(T_u\) 的权重最小(Line 17)。最终 KeyKG 将 \(T_{u_\textrm{min}}\) 作为结果返回。
算法 1 中的 getD 和
getSP
getD:计算两个顶点之间的距离。getSP:计算两个顶点之间的最短路径。
Running Example
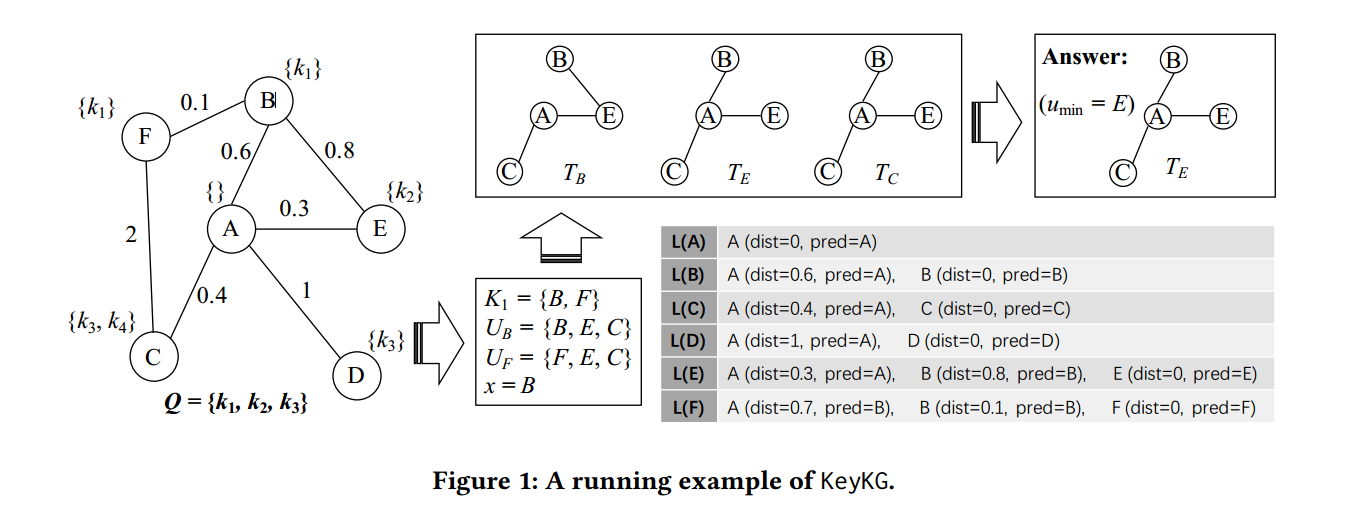
举个例子,如上图,给定一个查询 \(Q=\{k_1,k_2,k_3\}\) ,则 \(K_1=\{B,F\},\;K_2=\{E\},\;K_3=\{C,D\}\) 。
- 对于 \(B\in K_1\) ,\(E\) 必选;由于 \(\textrm{dist}(B,C) = 1 < 1.6 = \textrm{dist}(B,D)\) ,所以选择 \(C\) 。故 \(U_B = \{B,E,C\}\) 。
- 对于 \(B\in K_2\) ,\(E\) 必选;由于 \(\textrm{dist}(F,C) = 1.1 < 1.7 = \textrm{dist}(F,D)\) ,所以选择 \(C\) 。故 \(U_B = \{F,E,C\}\) 。
下面计算各自的权重之和:
- 对于 \(U_B\) ,\(W_B=\textrm{dist}(B,E)+\textrm{dist}(B,C) = 0.8+1 = 1.8\)
- 对于 \(U_F\) ,\(W_B=\textrm{dist}(F,E)+\textrm{dist}(F,C) = 0.9+1.1 = 2\)
由于 \(W_B < W_F\) ,故 \(x = B\) 。
接下来生成 GST :
- \(T_B\)
- 初始化 \(T_B\) 中仅有一个顶点 \(B\)
- 令 \(s_{\textrm{min}} = B\) ,则 \(t_{\textrm{min}} = E\) ,因为 \(\textrm{dist}(B,E) < \textrm{dist}(B,C)\)
- 令 \(t_{\textrm{min}} = C\) ,则 \(s_\textrm{min} = E\) ,因为 \(dist(E,C) < \textrm{dist}(B,C)\)
- 再求出相关最短距离的路径,将路径上的顶点和边加入 \(T_B\) ,即可得到图 KeyKG 执行的例子 中的 \(T_B\)
- \(T_E\) :类似 \(T_B\) 分析可得
- \(T_C\) :类似 \(T_B\) 分析可得
Static HL
Why we need Hub Labeling?
由上述介绍可知,KeyKG 依赖于两个子函数 getD 和
getSP
。在巨大的知识图谱中,一种直观的在线的实现这些子函数的方法(例如
Dijkstra
算法)的执行时间太长了;另一方面,离线生成每对顶点之间的距离和最短路径的空间开销十分大。为了权衡时空开销,这篇文章使用了
Hub Labeling ,一种离线生成的索引结构。
Basic Concept
一个静态的 HL 是一个图上的离线生成的索引结构。规范的说,对于一个图 \(G=<V,E>\) ,一个静态的 HL ,可以看作一个函数 \(L:V\mapsto 2^V\) ,它将顶点映射到顶点的集合(称作 hub),并且满足下列条件:
- \(\forall u,v\in V\) ,并且 \(u,v\) 在 \(G\) 中是连通的,\(\exists h\in L(u)\cap L(v)\) ,使得 \(h\) 在 \(u,v\) 之间的最短路径上
对于 \(\forall v\in V\) , \(L(v)\) 称为顶点 \(v\) 的标签。
Supporting For
Computing getD but not getSP
在标准的索引结构中,每一个 \(L(v)\)
是一个列表,其中包含按标识符排序的 hubs 。对于每一个 \(h\in L(v)\) ,\(\textrm{dist}(v,h)\)
也会预先计算出来并保存。这样我们就可以通过如下公式计算 getD
: \[
\textrm{getD}(u,v)=\begin{cases}
\underset{h\in L(u)\cap L(v)}{min} \textrm{dist}(u,h) +
\textrm{dist}(v,h) & L(u)\cap L(v) \ne \emptyset\\
\infty & L(u)\cap L(v) = \emptyset\\
\end{cases}
\] 其中,\(\textrm{dist}(u,h)\)
和 \(\textrm{dist}(v,h)\) 分别存储在
\(L(u)\) 和 \(L(v)\) 中。
但是,无法计算 getSP
Improvement in Construction
动机
从 \(\textrm{getD}(u,v)\)
计算公式来看,当索引标签较小时,getD
的在线计算会更快。但是,最小化索引标签的平均大小是一个 NP-Hard
问题,并且具有对数不可近似性(logarithmic
inapproximability)。给定一个图,有很多不同的启发式的方法能够构建合理的较小的索引标签。在其他的方法中,pruned
landmark labeling (PLL) 是一个非常热门的实现方法,它利用了 Dijkstra
算法,并且能够高效的剪枝达到缩小索引标签大小的目的。
算法

如算法 2 所示,标准的 PLL 基本流程是执行 Dijkstra 算法 \(n\) 次,其中 \(n\) 为顶点的个数(Line 3 - 24),并且在此过程中迭代地扩展顶点标签(Line 4,Line 12)。记 \(i\) 次迭代后 \(v\) 的标签为 \(L_i(v)\) 。在第 \(i\) 次迭代,Dijkstra 算法从一个不同的顶点 \(v_i\in V\) 出发(Line 7),访问其他顶点并且计算它们与 \(v_i\) 之间的距离,存储到 \(d\) 中(Line 14 - 15),再将 \(v_i\) 加入到它们的索引标签中。
关于剪枝
- 由于一些顶点 \(u\) 没有被访问到,所以它们的标签可以剪掉。
- 当 \(u\) 与 \(v_i\) 的距离可由构造好的 \(L_{i-1}\) 标签计算得到,也就是 Line 11 的条件为假,那么会发生剪枝。
改进:Betweenness Centrality
我们的目标是能够做更多剪枝来提高整个系统的性能。具体的,我们想要迭代早期构造的索引标签能够支持计算更多对顶点之间的距离,这样在后期的迭代过程中,就可以更频繁地发生剪枝操作。直观地,这可以通过这种方式实现,即在 Dijkstra 算法迭代的早期,选择那些许多最短路径都经过的顶点作为起始顶点。为了实现这个想法,原始的 PLL 实现方式是利用一些启发式的方法,对这些起始顶点按照其度数降序排列,因为高度数的顶点更有可能出现在许多顶点对之间的最短路径上。与传统方法不同,我们基于 betweenness centrality 对它们降序排序。顶点 \(v\) 的 betweenness centrality 定义如下: \[ \textrm{bc}(v)=\underset{s,\;t\in V\backslash\ \{v\}}{\sum}\frac{\sigma_{st}(v)}{\sigma_{st}} \] 其中,\(\sigma_{st}\) 表示顶点 \(s,\;t\) 之间最短路径的个数,\(\sigma_{st}(v)\) 表示上述路劲中经过顶点 \(v\) 的。
图上任意两个顶点之间的最短路径不止一条,因为可能存在最小权值相等但是路径不同的情况。

举个例子,如上图中的图。可以用 Floyd 算法计算出任意两顶点之间的最短距离和路径。之后依据这个信息和 betweenness centrality 的定义可得:
- \(\textrm{bc}(A) = 7\)
- \(\textrm{bc}(B)=4\)
- \(\textrm{bc}(C)=\textrm{bc}(D)=\textrm{bc}(E)=\textrm{bc}(F)=0\)
但是,论文中用了 [4] (TODO)中的近似算法来缩短计算时间。
构造 Static HL 的例子

假设图的结构如上图所示。
首先初始化 \(L_0(v)\) :
| \(L_0(A)\) | \(L_0(B)\) | \(L_0(C)\) | \(L_0(D)\) | \(L_0(E)\) | \(L_0(F)\) |
|---|---|---|---|---|---|
| \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) |
接着按照 betweenness centrality 对顶点降序排序,顺序为 A, B, C, D, E, F;
进入第一次循环:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) |
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| \(d[A]\) | \(d[B]\) | \(d[C]\) | \(d[D]\) | \(d[E]\) | \(d[F]\) |
|---|---|---|---|---|---|
| 0 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
PQ 优先队列为:
| A | NULL |
|---|---|
| 队头(队尾) |
进入内层 while 循环,
从 PQ 中弹出 \(A\) 赋给 \(u\) ,即 \(u=A\) ;
将 \(visit[u]\) 置 1,则:
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
利用 \(L_0\) 计算 \(\textrm{getD}(v_1,u)\) ,即计算 \(\textrm{getD}(A,A)\) 。由于 \(L_0(A)=\emptyset\) ,故 \(L_0(A)\cap L_0(A) = \emptyset\),所以 \(\textrm{getD}(A,A) = \infty\) (利用 \(\textrm{getD}\) 的公式可得)。
由于 \(\textrm{d}[u] = \textrm{d}[A] = 0 < \textrm{getD}(v_1,u)\) ,故 Line 11 的条件满足,进入条件体。
\(L_i(u)\leftarrow L_{i-1}(u)\cup\{v_i\}\) ,使得索引变化为:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) |
在接下来的对 \(u=A\) 未被访问的邻居顶点执行操作。
访问第一个邻居 \(B\) 后,\(d\) 变化如下:
| \(d[A]\) | \(d[B]\) | \(d[C]\) | \(d[D]\) | \(d[E]\) | \(d[F]\) |
|---|---|---|---|---|---|
| 0 | 0.6 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
则有属于 \(L_1(B)\) 的 \(A(\textrm{dist} = 0.6, \textrm{pred}= A)\) ,同时 B 插入到 PQ 中。
类似的,有
| \(d[A]\) | \(d[B]\) | \(d[C]\) | \(d[D]\) | \(d[E]\) | \(d[F]\) |
|---|---|---|---|---|---|
| 0 | 0.6 | 0.4 | 1 | 0.3 | \(\infty\) |
属于 \(L_1(C)\) 的 \(A(\textrm{dist} = 0.4, \textrm{pred}= A)\)
属于 \(L_1(D)\) 的 \(A(\textrm{dist} = 1, \textrm{pred}= A)\)
属于 \(L_1(E)\) 的 \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\)
在所有 A 的邻居访问完后,PQ 变为
| E | C | B | D | NULL |
|---|---|---|---|---|
| 队头 | 队尾 |
然后,回到 while 循环。
PQ 弹出 E,置 \(visit\) 为 1:
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0 |
由于 \(\textrm{d}[u] = \textrm{d}[E] = 0.3 < \textrm{getD}(v_1,u) = \textrm{getD}(A,E) = \infty\) ,故 Line 11 的条件满足,进入条件体。
\(L_i(u)\leftarrow L_{i-1}(u)\cup\{v_i\}\) ,使得索引变化为:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\) | \(\emptyset\) |
E 未访问的邻居为 B,但由于 \(d[u]+\text{wt}((u,w)) = d[E] + \text{wt}((E,B)) = 0.3 + 0.8 = 1.1 > d[B] = 0.6\),所以不更新;又由于 B 在 PQ 中,所以不加入 PQ。
此时 PQ 为:
| C | B | D | NULL |
|---|---|---|---|
| 队头 | 队尾 |
PQ 弹出 C,置 \(visit\) 为 1:
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 |
由于 \(\textrm{d}[u] = \textrm{d}[C] = 0.4 < \textrm{getD}(v_1,u) = \textrm{getD}(A,C) = \infty\) ,故 Line 11 的条件满足,进入条件体。
\(L_i(u)\leftarrow L_{i-1}(u)\cup\{v_i\}\) ,使得索引变化为:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \(\emptyset\) | \(A(\textrm{dist} = 0.4, \textrm{pred}= A)\) | \(\emptyset\) | \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\) | \(\emptyset\) |
C 未访问的邻居为 F,但由于 \(d[u]+\text{wt}((u,w)) = d[C] + \text{wt}((C,F)) = 0.4 + 2 = 2.4 < d[F] = \infty\),所以,更新 \(d[F]\) :
| \(d[A]\) | \(d[B]\) | \(d[C]\) | \(d[D]\) | \(d[E]\) | \(d[F]\) |
|---|---|---|---|---|---|
| 0 | 0.6 | 0.4 | 1 | 0.3 | 2.4 |
此时,属于 \(L_1(F)\) 的 \(A(\textrm{dist} = 2.4, \textrm{pred}= C)\)
又由于 F 不在 PQ 中,所以加入 PQ。
此时 PQ 为:
| B | D | F | NULL |
|---|---|---|---|
| 队头 | 队尾 |
PQ 弹出 B,置 \(visit\) 为 1:
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 |
由于 \(\textrm{d}[u] = \textrm{d}[B] = 0.6 < \textrm{getD}(v_1,u) = \textrm{getD}(A,B) = \infty\) ,故 Line 11 的条件满足,进入条件体。
\(L_i(u)\leftarrow L_{i-1}(u)\cup\{v_i\}\) ,使得索引变化为:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \[A(\textrm{dist} = 0.6, \textrm{pred}= A)\] | \(A(\textrm{dist} = 0.4, \textrm{pred}= A)\) | \(\emptyset\) | \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\) | \(\emptyset\) |
B 未访问的邻居为 F,但由于 \(d[u]+\text{wt}((u,w)) = d[B] + \text{wt}((B,F)) = 0.6 + 0.1 = 0.7 < d[F] = 2.4\),所以,更新 \(d[F]\) :
| \(d[A]\) | \(d[B]\) | \(d[C]\) | \(d[D]\) | \(d[E]\) | \(d[F]\) |
|---|---|---|---|---|---|
| 0 | 0.6 | 0.4 | 1 | 0.3 | 0.7 |
此时,属于 \(L_1(F)\) 的 \(A(\textrm{dist} = 0.7, \textrm{pred}= B)\)
又由于 F 在 PQ 中,所以不加入 PQ。
此时 PQ 为:
| D | F | NULL |
|---|---|---|
| 队头 | 队尾 |
PQ 弹出 D,置 \(visit\) 为 1:
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0 |
由于 \(\textrm{d}[u] = \textrm{d}[D] = 1 < \textrm{getD}(v_1,u) = \textrm{getD}(A,D) = \infty\) ,故 Line 11 的条件满足,进入条件体。
\(L_i(u)\leftarrow L_{i-1}(u)\cup\{v_i\}\) ,使得索引变化为:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \[A(\textrm{dist} = 0.6, \textrm{pred}= A)\] | \(A(\textrm{dist} = 0.4, \textrm{pred}= A)\) | \(A(\textrm{dist} = 1, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\) | \(\emptyset\) |
D 没有未访问的邻居,故不更新 \(d[F]\) ,也就没有顶点加入 PQ。
此时 PQ 为:
| F | NULL |
|---|---|
| 队头(队尾) |
PQ 弹出 F,置 \(visit\) 为 1:
| \(visited[A]\) | \(visited[B]\) | \(visited[C]\) | \(visited[D]\) | \(visited[E]\) | \(visited[F]\) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
由于 \(\textrm{d}[u] = \textrm{d}[F] = 0.7 < \textrm{getD}(v_1,u) = \textrm{getD}(A,F) = \infty\) ,故 Line 11 的条件满足,进入条件体。
\(L_i(u)\leftarrow L_{i-1}(u)\cup\{v_i\}\) ,使得索引变化为:
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \[A(\textrm{dist} = 0.6, \textrm{pred}= A)\] | \(A(\textrm{dist} = 0.4, \textrm{pred}= A)\) | \(A(\textrm{dist} = 1, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.7, \textrm{pred}= B)\) |
F 没有未访问的邻居,故不更新 \(d[F]\) ,也就没有顶点加入 PQ。
此时 PQ 为:
NULL |
|---|
至此,第一次 for 迭代结束,索引结果为
| \(L_1(A)\) | \(L_1(B)\) | \(L_1(C)\) | \(L_1(D)\) | \(L_1(E)\) | \(L_1(F)\) |
|---|---|---|---|---|---|
| \(A(\textrm{dist} = 0, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.6, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.4, \textrm{pred}= A)\) | \(A(\textrm{dist} = 1, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.3, \textrm{pred}= A)\) | \(A(\textrm{dist} = 0.7, \textrm{pred}= B)\) |
类似的处理,可得下图右下角的索引。

Extension of Index Structure
为了支持计算 getSP ,我们需要扩展 L
的索引结构。在算法 2 中,对于每一个 hub \(v_i\in L(w)\) ,我们不仅仅存储了 \(\textrm{dist}(w,v_i)\) ,还存储了以 \(v_i\) 为根节点搜索树中 \(w\) 的前驱顶点,并将其记作 \(\textrm{pred}(w,v_i)\) (Line 16)。
有了扩展后的索引结构,getSP 就可以通过算法
3 计算得到。为了得到顶点 \(u,\;v\) 之间的一条最短路径 \(p\) ,我们首先在 \(p\) 上找到它们所共有的 hub \(h_{\textrm{min}}\) (Line
1),然后重复地跟随前驱顶点,构造路径 \(p\) 的从 \(u\) 到 \(h_{\textrm{min}}\) 的一段(Line 2-8),以及
\(v\) 到 \(h_{\textrm{min}}\) 的一段(Line
9-14)。


举个例子,比如计算 getSP(D, F) 。
首先,L(D) 和 L(F) 的公共 hub
只有一个,就是 \(A\),则 \(h_{\textrm{min}} = A\) 。
然后,通过 pred 信息找到 D-A 的路径,为 D-A ,因为
L(D) 中 \(A\) 的
pred 为 \(A\)。
接着,同样的,找到 F-A 的路径,为 F-B-A,因为 L(F) 中的
A 的 pred 为 \(B\),L(B)
中的 \(A\) 的 pred 为
\(A\)。
最后,将上面两个子路径连起来,我们就找到了路径 \(p\),为 D-A-B-F。
KeyKG+ With Dynamic HL
Dynamic HL
Features
- 查询相关的(query-relevant)
- 在线构造的(online constructed)
Definition and structure
一个动态 HL 是一个 \((g-1)\times n\) 的矩阵,记作 \(M\) 。行对应于关键词顶点集 \(K_2,K_3,\dots,K_g\) ,列对应于 hub 顶点。\(M\) 的第 \((i-1)\) 行(记作 \(M_{i-1}\))倒排并且聚集了 \(K_i\) 中顶点的静态索引标签。\(M_{i-1}\) 的第 j 个元素(记作 \(M_{i-1,j}\))是非空的,如果 \(h_j\in V\) 是一个 hub,并且它在 \(K_i\) 的至少一个顶点的静态索引标签中。在 \(K_i\) 中的这些顶点中(这些顶点的静态索引标签包括 \(h_j\)),\(M_{i-1, j}\) 代表了最小化到达 \(h_j\) 的距离的顶点。如果, \(h_j\) 不是一个在 \(K_i\) 中任意一个顶点的索引标签中的 hub,那么我们令 \(M_{i-1, j}\) 为 null: \[ M_{i-1,j}=\begin{cases} &\underset{u\in K_i\; s.t.\; h_j\in L(u)}{\textrm{argmin}}\textrm{dist}(u, h_j)&h_j\in \bigcup_{u\in K_i}L(u),\\ &null&h_j\not\in \bigcup_{u\in K_i}L(u), \end{cases} \] 具体的,论文中使用二维数组存储矩阵 \(M\) ,因此可以支持常数时间的随机访问。对于每一个不为 null 的 \(M_{i-1, j}\) ,与 \(h_j\) 的距离也是先计算出来,并保存到 \(M\) 中。
Example

- \(i = 2\) 时,\(K_2=\{E\}\) ,\(L(E) = \{A,B,E\}\) ,因此矩阵 \(M\) \(K_2\) 行只有 \(A,B,E\) 不为 null,其他都为 null;由于 \(K_2\) 中只有一个元素 \(E\) ,故 \(K_2\) 行 \(A,B,E\) 列中的元素都为 \(E\) 和到它的距离(从 \(L(E)\) 中直接取得)。
- \(i = 3\) 时,\(K_3=\{C,D\}\) ,\(L(C)\cup L(D) = \{A,C,D\}\) ,因此矩阵 \(M\) \(K_3\) 行只有 \(A,C,D\) 不为 null,其他都为 null;由于 \(K_3\) 中有两个元素,故 \(K_3\) 行 \(A,C,D\) 列中的元素需要对比一下分别到 \(C\) 和 \(D\) 的距离,选择较小的存入矩阵 \(M\) (比如 \(M_{K_3, A}\) ,由于 \(\textrm{dist}(C,A) < \textrm{dist}(D,A)\),所以将 \(C\) 存入矩阵)。
综上所示,矩阵 \(M\) 如下图所示:

Algorithm KeyKG+
Algorithm Explained
KeyKG+ 如算法 4 所示。这个算法主要构造了动态 HL,并将其使用在两个方面,提高执行的总体性能,并且对最终结果没有任何影响。

在第一部分,首先,为 \(K_2,\dots,K_g\) 构造矩阵 \(M\) (Line 1-3)。然后,按照如下流程利用 \(M_{i-1}\) 找到 \(v_i\) (Line 6)。对于每一个 hub \(h_j\in L(v_1)\) ,我们从 \(L(v_1)\) 中取得 \(\textrm{dist}(v_1,h_j)\) ,并且从 \(M_{i-1}\) 中取 \(M_{i-1, j}\) 元素的 \(\textrm{dist}(M_{i-1,j},h_j)\) 。如果 \(M_{i-1,j}\) 非空,那么我们计算: \[ \textrm{dist}(v_1,h_j)+\textrm{dist}(M_{i-1,j},h_j) \] 这个结果表示了 \(v_1\) 到在 \(K_i\) 中经过一个特定的 \(h_j\) 所能到达的顶点之间的最短距离。最后, 通过如下方式,找到 \(v_i\) : \[ v_i=\underset{M_{i-1, j}\; s.t.\; h_j\in L(v_1)\; \textrm{and}\; M_{i-1, j}\ne \textrm{null}}{\textrm{argmin}} \textrm{dist}(v_1,h_j)+\textrm{dist}(M_{i-1,j},h_j) \] KeyKG+ Line 6 计算得到的 \(v_i\) 和 KeyKG Line 3 得到的 \(v_i\) 等价,但是 KeyKG+ 的效率更高。
第二部分,我们像为 \(K_i\) 创建 \(M_{i-1}\) 一样,为 \(V_{T_u}\) (Line 14)创建 \(M'_{u}\) 。随着 \(T_u\) 在每次迭代中逐渐扩展(Line 21),\(M'_{u}\) 通过加入到 \(T_u\) 的顶点的静态索引标签得到更新(Line 22)。对于每一个 \(t_i\in(U_x\backslash V_{T_u})\) ,\(M'_u\) 被用来找到与 \(t_i\) 距离最短的顶点 \(s_i\in V_{T_u}\) (Line 16-18)。我们在所有的这样的 \(<s_i,t_i>\) 中找到最小的 \(<s_{\textrm{min}},t_{\textrm{min}}>\) (Line 19)
KeyKG+ Line 16-19 计算得到的 \(<s_{\textrm{min}},t_{\textrm{min}}>\) 和 KeyKG Line 12 得到的 \(<s_{\textrm{min}},t_{\textrm{min}}>\) 等价,但是 KeyKG+ 的效率更高。
Running Example

如上图,
- 令 \(B\in K_1\) 为 \(v_1\) ,查询其 Static HL,得到 \(L(B) = \{A,B\}\) ;
- 因为 \(M_{1,A} = M_{1,B} = E\) ,所以令 \(E\in K_2\) 为 \(v_2\) ;
- 因为 \(M_{2,A} = C, M_{2,B} = \textrm{null}\) ,所以令 \(C\in K_3\) 为 \(v_3\) ;
- 这样就形成了 \(U_B=\{B,E,C\}\) (这与算法 KeyKG 得到的结果是一致的)
- 令 \(F\in K_1\) 为 \(v_1\) ,查询其 Static HL,得到 \(L(F) = \{A,B,F\}\) ;
- 因为 \(M_{1,A} = M_{1,B} = E, M_{1,F} = \textrm{null}\) ,所以令 \(E\in K_2\) 为 \(v_2\) ;
- 因为 \(M_{2,A} = C, M_{2,B} = M_{2,F} = \textrm{null}\) ,所以令 \(C\in K_3\) 为 \(v_3\) ;
- 这样就形成了 \(U_F=\{F,E,C\}\) (这与算法 KeyKG 得到的结果是一致的)
TODO:另一半的例子怎么解释???
How much?
- 基于 betweenness centrality 的启发式方法构建的 Static Hub Labelings 超越了现存的方案。
- Dynamic Hub Labelings 则通过倒排并聚集查询相关的静态标签,加速了总体的查询效率。
What Then?
- 寻找支持更高效地边删除(edge deletion)的解决方案
- KeyKG+ 的近似比率可以进一步得到提高
- 现存 HL 方案无法处理巨大而稠密的图。
Problems to Solve
Ittai Abraham, Daniel Delling, Andrew V. Goldberg, and Renato Fonseca F. Werneck. 2011. A Hub-Based Labeling Algorithm for Shortest Paths in Road Networks. In SEA. 230–241.↩︎
Takuya Akiba, Yoichi Iwata, and Yuichi Yoshida. 2013. Fast exact shortest-path distance queries on large networks by pruned landmark labeling. In SIGMOD. 349–360↩︎
Takuya Akiba, Yoichi Iwata, and Yuichi Yoshida. 2013. Fast exact shortest-path distance queries on large networks by pruned landmark labeling. In SIGMOD. 349–360↩︎
Ulrik Brandes. 2001. A faster algorithm for betweenness centrality. J. Math. Soc. 25, 2 (2001), 163–177.↩︎
Ziyad AlGhamdi, Fuad Jamour, Spiros Skiadopoulos, and Panos Kalnis. 2017. A Benchmark for Betweenness Centrality Approximation Algorithms on Large Graphs. In SSDBM↩︎