CosmosNing的个人博客

探索·好奇

0%

去目的地的最短路径怎么算（上）

发表于 更新于 分类于
本文字数： 3.7k 阅读时长 ≈ 3 分钟
介绍一些求最短路径的算法

引入

cover

上两篇文章中，我们具体讨论了“去目的地的最少中转方案”这个问题，并给出算法过程以及它的实现。在实际生活中，我们对于出行方案的需求除了“最少中转”，还有“最短路径”。今天，我们一起来思考一下如何计算出去目的地的最短路径。

问题分析

在地图中，从某一位置到达另一个位置通常有很多条路径。其中，总路径长度最短的，叫做“最短路径”。

“最短路径”是这个问题的输出，也是这个问题的目标。为了达到这个目标，第一步就需要我们搞清楚它的输入是什么（或者我们能提供什么样的原始信息【通常是可测量的】），在这个基础之上我们才能运用或者设计合适的算法，给出符合期望的结果。

在前两篇文章中，我们一起了解到，图这种数据结构，天生地可以表示多个点之间多对多的关系。因而，在这个问题中，我们通过图存储信息。与之前的图略有不同的是，这里的图还存储有两个相邻点之间路径的代价（在这个问题中，就是该道路的长度）。这样的图，在每一条边上都有对应的值（称作“权值”），也被称作为“网”。这个由各个道路长度、各个顶点和边构成的交通网以及用户给定的起点、终点信息，作为我们的输入。

那么，如何利用这个输入信息得到我们希望的结果呢？这里就要用到 Dijkstra 算法。

Dijkstra 算法

Dijkstra 算法描述如下：

  1. 找到所花代价最小的顶点。这个顶点满足，从起点开始到达该顶点的路径长度最短。
  2. 更新第一步找到顶点的邻居顶点的代价（这个代价是指从起点到该顶点的距离加上该顶点到相应邻居顶点的距离）。
  3. 重复上述操作，直至每一个顶点都被处理过。
  4. 计算最终路径，给出指定要求的输出

上面的算法描述太过抽象，我们看一个例子来体会一下这个算法的过程。

假设，一个简单的交通网如下所示：

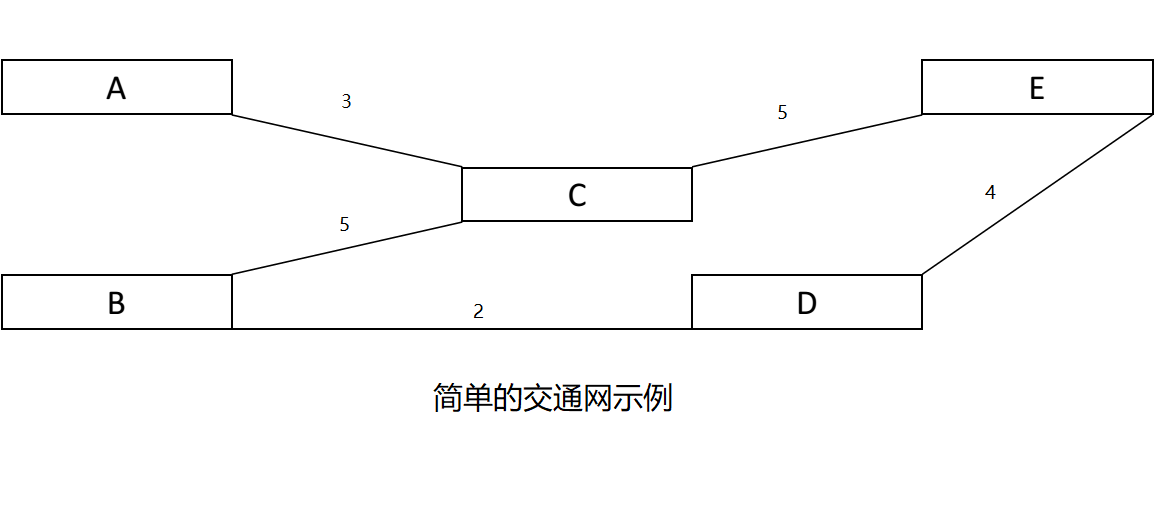
简单的交通网示例

比如，用户想要从 A 到 D 的最短路径。

在利用 Dijkstra 算法之前，首先要对相关数据初始化。初始时，我们有如下表格：

顶点 从起点到达该点的最短路径长度
A（已处理） \(\infty\)
B \(\infty\)
C 3
D \(\infty\)
E \(\infty\)

第一步，找到符合要求的顶点 C 。

第二步，更新 C 邻居顶点的的代价（也就是B、E【A是起点，不参与更新】）。从而有以下表格：

顶点 从起点到达该点的最短路径长度
A（已处理） \(\infty\)
B \(3 + 5 = 8\) （由于\(3 + 5 = 8 < \infty\) ，所以更新）
C（已处理） 3
D \(\infty\)
E \(3 + 5 = 8\)（由于\(3 + 5 = 8 < \infty\) ，所以更新）

重复第一步，找到符合要求的顶点 B 。

又是第二步，更新 B 邻居顶点的代价（也就是 C 和 D ）。从而有以下表格：

顶点 从起点到达该点的最短路径长度
A（已处理） \(\infty\)
B（已处理） 8
C（已处理） 3（由于\(8 + 5 > 3\) ，所以不更新）
D \(8 + 2 = 10\)（由于\(8 + 2 = 10 < \infty\) ，所以更新）
E 8

重复第一步，找到符合要求的顶点 E 。

又是第二步，更新 E 邻居顶点的代价（也就是 C 和 D ）。从而有以下表格：

顶点 从起点到达该点的最短路径长度
A（已处理） \(\infty\)
B（已处理） 8
C（已处理） 3（由于\(8 + 5 > 3\) ，所以不更新）
D 10（由于 \(8 + 4 > 10\) ，所以不更新）
E（已处理） 8

最后一个满足要求的点为 D ，经过算法处理完的表格结果如下：

顶点 从起点到达该点的最短路径长度
A（已处理） \(\infty\)
B（已处理） 8（由于 \(10 + 2 > 8\) ，所以不更新）
C（已处理） 3
D（已处理） 10
E（已处理） 8（由于\(10 + 4 > 8\) ，所以不更新）

到此为止，我们可以在表给中找到，从 A 到 D 的最短路径长度为 10 。简单地检验一下，这个结果是正确的。除了给出最短路径长度，我们还需要给出路径方案。靠上述中的表格信息远远不够。

那么如何计算出最短路径方案呢？还记得上一篇文章中我们是如何给出最少中转方案的吗？通过引入名为 parents 的哈希表，将当前路径点和上一个顶点联系起来。 在算法处理过程中，更新这个哈希表。算法处理完后，从终点开始，一个个寻找它的上一个顶点，直至到达起点。最后将这些路径点按照从起点到终点的顺序排列，存储起来或者直接输出。

至此，想必大家对 Dijkstra 算法执行的过程有所了解，下面便是代码实现环节。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
# 建立图
graph = {}
graph['A'] = {'C': 3}
graph['B'] = {'C': 5, 'D': 2}
graph['C'] = {'A': 3, 'B': 5, 'E': 5}
graph['D'] = {'B': 2, 'E': 4}
graph['E'] = {'C': 5, 'D': 4}

# 新建parents哈希表，将当前路径点和上一个顶点联系起来
parents = {}

# 存储图上的点是否被访问过。
# 如果某点在searched集合中，那么该点在之前已经被访问过；
# 否则，没有
searched = []

# 定义常量：无穷大
infinity = float('inf')

# 新建costs哈希表，记录每一个顶点和从起点到达该顶点的最短路径长度
costs = {}


def find_lowest_cost_node(m_costs):
    """
    在m_cost中寻找未被搜索过并且所花代价最小的结点
    :param m_costs: 道路代价集合
    :return: 符合要求的结点
    """
    lowest_cost = float('inf')
    lowest_cost_node = None
    for node in m_costs:
        cost = m_costs[node]
        if cost < lowest_cost and node not in searched:
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node


def dijkstra(src, des):
    """
    利用dijkstra算法，寻找图中从src点到des点的最短路径
    :param src: 起点
    :param des: 终点
    :return: 路径方案(list), 最短路径长度
    """
    # 根据起点信息，更新parents和costs
    for key in graph.keys():
        if key in graph[src].keys():
            parents[key] = src
            costs[key] = graph[src][key]
        else:
            parents[key] = None
            costs[key] = infinity

    # 寻找所花代价最小的结点，分情况更新parents和costs
    node = find_lowest_cost_node(costs)
    while node is not None:
        cost = costs[node]
        neighbors = graph[node]
        for n in neighbors.keys():
            new_cost = cost + neighbors[n]
            if costs[n] > new_cost:
                costs[n] = new_cost
                parents[n] = node
        searched.append(node)
        node = find_lowest_cost_node(costs)

    # 根据parents信息和起点信息找出最短路径。
    stack = []
    road = []
    stack.append(des)
    child = des
    while parents[child] != src:
        stack.append(parents[child])
        child = parents[child]
    stack.append(src)
    while stack:
        road.append(stack.pop())

    # 返回路径方案和最短路径长度。
    return road, costs[des]

# 测试例程
if __name__ == '__main__':
    r, c = dijkstra('A', 'D')

    print("最短路径：")
    print("->".join(r))
    print("路径长度：")
    print(c)

总结

今天，我和你一起通过计算最短路径这个问题，探讨了 Dijkstra 算法的执行流程和算法实现。我将这篇文章的要点总结如下：

  1. 对于边有权值的图，我们通常将其称作"网"。一个“网”的实例就是地图中的交通网络

  2. Dijkstra 算法可以用来计算“网”中从某一点到另一点所花代价最小的方案。在地图中，就是用来计算两个点之间的最短路径方案

思考

Dijkstra 算法可以处理所有情况下的最短路径问题吗？这个问题留给你思考，欢迎你留言与我一起讨论。