CosmosNing的个人博客

探索·好奇

0%

去目的地的最短路径怎么算（下）

发表于 更新于 分类于
本文字数： 6k 阅读时长 ≈ 5 分钟
Dijkstra 算法是对于最短路径问题是万能的吗？

Dijkstra 算法的局限性

cover

上一篇文章中，我给你留下一个思考题：

Dijkstra 算法可以处理所有情况下的最短路径问题吗？

你的答案是什么呢？如果是不是，那么恭喜你，你答对了。

那么在什么情况下， Dijkstra 算法不再适用呢？我们一起来看一个具体的例子。

假设有6个人，分别是 A 、B 、C 、D 、E 、F 。他们每个人都有一个十分珍爱的东西，除非用他们自己所认为的等价的东西交换，否则一般情况下，他们是不卖这些东西的。

有一天，A 突然想要用自己所珍爱的东西换取 F 的东西。于是， A 边和 F 商量，自己的东西是否能作为交换的等价物。可是，非常遗憾， F 看不上 A 的东西，并不同意。

故事到了这里，并没有结束。 A 非常执( nan )着( chan )， F 被他的精神打动了，做出一定的妥协。 F 说，如果你能用你的东西换到 C 的东西，并且加上 1 块钱，我就和你换。

A 非常激动，跑去找 C 。结果也是被拒。直接交换不成功，那么就间接交换吧， A 如是提议着。C 想了想，自己也有想要拥有其他人的一些东西，便提出了自己的要求：如果你能换到 E 的东西，我能返你 6 快钱；如果你能换到 B 的东西，那么还要在加上 1 块钱。

A 又去找 B 、E 商量，他们也提出了自己的要求。

最终 A 把这些信息化成一张图，构成如下所示的交换贸易网：

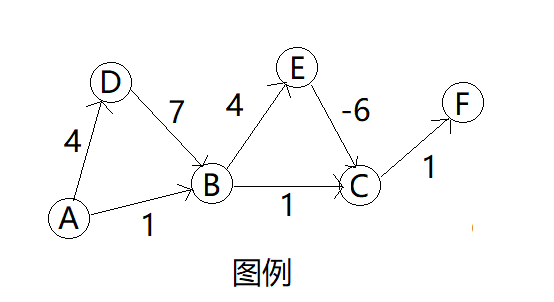
graph

那么，现在问题来了， A 如何能画最少的钱，用自己的东西换到 F 的东西呢？

仔细分析题目中抽象出的交换网以及问题，这不就是在求有权图（或者是网）中，从某一点到另一点的最短路径方案嘛，直接用 Dijkstra 算法就能解决！

我们把这里的网输入交给 Dijkstra 算法计算一下，它的输出又是什么呢？

1
2
3
4
5
# 输出结果
最短路径：
A->B->C->F
路径长度：
3

惊了！该算法怎么没走含有负数的路径，原本代价可以更小的！那这个算法究竟哪里存在不足呢？仔细分析一下， Dijkstra 算法在寻找最短路径时，是存在一些“短见”的。它考虑最短路径是依据起点到当前点的最短距离加上该点到其邻居节点的距离。依据这个和，找到和最小的邻居结点，并选择这个点作为下一个点。在这种情况下，它并不会考虑到下几个结点的和会出现更小的情况。以上面的例子来说，在到达B时，算法在选择 C 或者 E 作为下一个最短路径的结点时，更倾向于贪心地选择下一个结点代价更小的 C ，而不会选择下两个结点和会更小的 E 。

那为什么上次在计算最短路径时， Dijkstra 算法表现的十分出色呢？原来在所有边的权值都为正数时，是不会出现上述情况的。所以 Dijkstra 算法在边权值为负数的时候，可能会出现错误。

那么对于负数边的图，怎样计算其中的最短路径呢？这就要用到 Floyd 算法。

Floyd 算法1

试想有一个图，它有 N 个顶点，编号从 1 到 N 。我们设 shortestPath(i, j, k) 为一条最短路径，这条最短路径从 i 出发 到 j 为止，并且中间只经过 {1, 2, ···, k} 这些点。那么图上的最短路径问题即可描述为，对于每一个 i 、 j 对， 寻找它们之间的最短路径，其中间路径只通过 {1, 2, ···, N} ，也就是对每一组 i, j ,求 shortestPath(i, j, N) 。

对 shortestPath(i, j, k) 这个式子的含义进一步分析，不难发现，它的结果不外乎两种情况：

  1. 路径并不通过顶点 k （也就是可用顶点集合为 {1, 2, ···, k-1} ）
  2. 路径通过顶点 k （路径先从 i 开始，到 k 暂停；再从 k 开始，最终到达终点 j 。其中间只经过 {1, 2, ···, k-1} ）

将上述两点，结合开头的定义将这个问题进一步化简，对于 shortestPath(i, j, k) ，它可能的解可以用如下式子表示

  1. shortestPath(i, j, k-1)
  2. shortestPath(i, k, k-1) + shortestPath(k, j, k-1)

也就是

\[ \begin{aligned} shortestPath(i, j, k) = min(&shortestPath(i, j, k-1),\\ &shortestPath(i, k, k-1) + shortestPath(k, j, k-1) ) \end{aligned} \] 上述式子是一个递推公式，那么它一定有一个起始值。在这里，k = 0 条件下的值便是它的起始值。用公式便可表示如下：

\[ shortestPath(i, j, 0) = w(i, j) \]

这种情况下，为 i 和 j 两点直接相连。其中， w(i, j) 为顶点为 i 、j 边上的权值。

将上述两个式子写到一起，便是

\[ shortestPath(i, j, k) = \left \{ \begin{aligned} & w(i, j), &k = 0\\ & min \left ( \begin{aligned} &shortestPath(i, j, k-1),\\ &shortestPath(i, k, k-1) + shortestPath(k, j, k-1) \end{aligned} \right ) , &k > 0\\ \end{aligned} \right. \]

上式便是 Floyd 算法的核心公式。当算法运行时，对于每一组顶点 i 和顶点 j 的组合，计算每一个 k 取值情况下的 shortestPath 值。当用户查询时，只需从 shortestPath 中访问即可。

实现

这个算法如何实现呢？

我们先来看下维基百科上的伪代码描述

source2 

1
2
3
4
5
6
7
8
9
10
11
let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
for each edge (u,v)
    dist[u][v] ← w(u,v)  // the weight of the edge (u,v)
for each vertex v
    dist[v][v] ← 0
for k from 1 to |V|
    for i from 1 to |V|
       for j from 1 to |V|
          if dist[i][j] > dist[i][k] + dist[k][j] 
             dist[i][j] ← dist[i][k] + dist[k][j]
          end if

以这个为基础，很容易将它转成 Python 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import numpy as np # 在你的终端命令行中输入 'pip install numpy' 命令安装numpy包。已经安装过的可以忽略

# 建立图
graph = {}
graph['A'] = {'B': 1, 'D': 4}
graph['B'] = {'C': 1, 'E': 4}
graph['C'] = {'F': 1}
graph['D'] = {'C': 3}
graph['E'] = {'C': -6}
graph['F'] = {}

# 定义常量
A, B, C, D, E, F = list(range(len(graph))) 

# 将字符映射到对应的常量
index = {'A' : A, 'B' : B, 'C' : C, 'D' : D, 'E' : E, 'F' : F} 


def floyd():
    """
    利用 floyd 算法，计算图中任意两点间的最短路径长度，并以矩阵的形式打印出来
    :return: 无
    """
    V = len(graph)
    dist = np.array([[np.inf] * V] * V)   # 保存最短路径距离
    
    for u in graph.keys():
        dist[index[u]][index[u]] = 0
        for v in graph[u].keys():
            dist[index[u]][index[v]] = graph[u][v]
    
    for k in range(V):
        for i in range(V):
            for j in range(V):
                if dist[i][j] > dist[i][k] + dist[k][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]

    print(dist)

if __name__ == '__main__':
    floyd()
"""
输出结果
[[  0.   1.  -1.   4.   5.   0.]
 [ inf   0.  -2.  inf   4.  -1.]
 [ inf  inf   0.  inf  inf   1.]
 [ inf  inf   3.   0.  inf   4.]
 [ inf  inf  -6.  inf   0.  -5.]
 [ inf  inf  inf  inf  inf   0.]]
"""

上述实现仅仅给出了最短路径长度，有时候我们更需要的是最短路径的方案。怎么办呢？

维基百科中进一步给出了如下的伪代码描述：

source3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
let dist be a |V| × |V| array of minimum distances initialized to ∞
 (infinity)
let next be a |V| × |V| array of vertex indices initialized to null

procedure FloydWarshallWithPathReconstruction ()
   for each edge (u,v)
      dist[u][v] ← w(u,v)  // the weight of the edge (u,v)
      next[u][v] ← v
   for k from 1 to |V| // standard Floyd-Warshall implementation
      for i from 1 to |V|
         for j from 1 to |V|
            if dist[i][j] > dist[i][k] + dist[k][j] then
               dist[i][j] ← dist[i][k] + dist[k][j]
               next[i][j] ← next[i][k]

procedure Path(u, v)
   if next[u][v] = null then
       return []
   path = [u]
   while u ≠ v
       u ← next[u][v]
       path.append(u)
   return path

所以有 Python 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import numpy as np # 在你的终端命令行中输入 'pip install numpy' 命令安装numpy包。已经安装过的可以忽略

# 建立图
graph = {}
graph['A'] = {'B': 1, 'D': 4}
graph['B'] = {'C': 1, 'E': 4}
graph['C'] = {'F': 1}
graph['D'] = {'C': 3}
graph['E'] = {'C': -6}
graph['F'] = {}

# 定义常量
A, B, C, D, E, F = list(range(len(graph))) 

# 将字符映射到对应的常量
index = {'A' : A, 'B' : B, 'C' : C, 'D' : D, 'E' : E, 'F' : F} 


def floyd_with_path_reconstruction(src, des):
    """
    利用 floyd 算法，计算图中两点间的最短路径长度，和路径方案
    :param src: 起点
    :param des: 终点
    :return: 路径方案（列表），最短路径长度（一个数）
    """
    V = len(graph)
    dist = np.array([[np.inf] * V] * V)  # 保存最短路径距离
    next_ = np.array([[None] * V] * V)  # 保存当前路径上的下一个顶点

    for u in graph.keys():
        dist[index[u]][index[u]] = 0
        for v in graph[u].keys():
            dist[index[u]][index[v]] = graph[u][v]
            next_[index[u]][index[v]] = v
    
    for k in range(V):
        for i in range(V):
            for j in range(V):
                if dist[i][j] > dist[i][k] + dist[k][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]
                    next_[i][j] = next_[i][k]

    # 生成路径方案
    if next_[index[src]][index[des]] is None:
        return [], np.inf
    path = [src]
    u = src
    while u != des:
        u = next_[index[u]][index[des]]
        path.append(u)

    # 返回结果
    return path, dist[index[src]][index[des]]

# 测试例程
if __name__ == '__main__':
    r, c = floyd_with_path_reconstruction('A', 'F')

    print("最短路径：")
    print("->".join(r))
    print("路径长度：")
    print(c)
"""
输出结果
最短路径：
A->B->E->C->F
路径长度：
0.0
"""

上述的最终结果符合我们的预期。

复杂度分析

由于 Floyd 算法中存在一个非常消耗时间的三重循环，所以该算法的时间效率并不高，其时间复杂度为 \(O(N^{3})\) 。

总结

今天我从一个非常有意思的例子和你一起了解到 Dijkstra 算法的局限性，由此引出客服其局限性的 Floyd 算法，并且介绍了它的算法思想和算法实现。

最后，我将本文的要点总结如下：

  1. 在边权值全部为正数的图中求最短路径，适合使用 Dijkstra 算法；
  2. 在边权值存在负数的图中求最短路径，应该使用 Floyd 算法；
  3. Floyd 算法 的时间复杂度为 \(O(N^{3})\) 。
  4. Dijkstra 算法的时间复杂度为 \(O(N^{2})\) 。（这个小知识点，我上篇文章忘说了，你可以自己推导下）

  1. https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm#Algorithm↩︎

  2. https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm#Algorithm↩︎

  3. https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm#Path_reconstruction↩︎