统计学习框架及经验风险最小化

本文主要介绍两个内容：

1. 统计学习框架。这是一个十分通用的框架，指明了学习的输入、输出和学习目标。
2. 经验风险最小化（ERM）的学习方法。引入经验风险，从而可以从训练数据中管中窥豹，归纳出一般规律。但是 ERM 会产生过拟合现象。一种常见的解决方案是引入归纳偏好（或者是先验知识）。具体来说，确定一个有限的假设类集合，供学习算法学习。这样是否是有效的？通过证明发现，只要有足够的训练样本，就可以达到比较好的效果。

A Formal Model —— The Statistical Learning Framework

The Learner's Input

• 领域集（Domain set）：这是我们希望标记的事物的集合，记作 \(\mathcal{X}\) 。通常情况下，人们会用一个特性向量（vector of features）表示这些领域点（domain points）。

• 领域集（domain set）又称作实例空间（instance space）
• 领域点（domain points）又称作实例（instances）

• 标签集（Label set）：这是可能的标签的集合，记作 \(\mathcal{Y}\) 。
• 训练数据（Training data）：这是一系列已经被标记的领域点，常常表示为 \(S=((x_1,\ y_1)\dots(x_m,\ y_m))\) （这是在 \(\mathcal{X}\times \mathcal{Y}\) 中的有限的数对序列）

• 训练数据（training data）又称作 training examples，或者 training set

The Learner's Output

人们希望学习器输出一个预测规则（prediction rule）：\(h:\mathcal{X} \rightarrow \mathcal{Y}\) 。这个函数又称作为预测器（predictor）、假设（hypothesis）或者是分类器（classifier）。此外，我们记一个学习算法 \(A\) ，接受训练数据 \(S\) 为输入，返回对应假设为 \(A(S)\) 。

A Simple Data-generation Model

训练数据是如何生成的？这里给出两个假设。

• 假设所有的实例都由一个概率分布生成，记这个在 \(\mathcal{X}\) 上的概率分布为 \(\mathcal{D}\) 。
• 假设存在一个“完全正确”的标记函数 \(f:\mathcal{X}\rightarrow \mathcal{Y}\) ，显然，对于任意的 \(i\) ，有 \(y_i=f(x_i)\)

总的来说，在训练数据中的每一个数对，都由以下方式生成：

1. 先从概率分布 \(\mathcal{D}\) 采样得到一个点 \(x_i\) ；
2. 再利用标记函数 \(f\) 为 \(x_i\) 打上标签。

Measures of Success

如何衡量算法学习是否成功？这里可以定义一个分类器的误差（error of a classifier），即学习算法没有正确预测随机数据（这些随机数据，是由前面提到的对于学习算法隐含的概率分布所生成的）的标签的概率。也就是说，\(h\) 的误差是从分布 \(\mathcal{D}\) 随机中取出一个 \(x\) ，而 \(h(x)\) 不等于 \(f(x)\) 的概率。

规范的来讲，给定一个领域子集（domain subset），\(A\subset \mathcal{X}\) ，概率分布 \(\mathcal{D}\) ，定义一个数 \(\mathcal{D}(A)\) ，其中 \(\mathcal{D}(A)\) 表示学习算法在 \(\mathcal{D}\) 中观察到一个点 \(x\in A\) 的可能性。我们定义预测规则（prediction rule）的误差如下： \[ L_{\mathcal{D},f}(h)\overset{def}{=}\underset{x\sim\mathcal{D}}{\mathbb{P}}[h(x)\ne f(x)]\overset{def}{=}\mathcal{D}(\lbrace x:h(x)\ne f(x)\rbrace)\tag{2.1} \]

有关 \(A\) 与 \(\mathcal{D}(A)\) 的补充说明

• 在许多情况下，我们将 \(A\) 称作一个事件（event）
• 二元分类问题中，我们定义 \(A\) 为 \(\pi :\mathcal{X}\rightarrow \lbrace0,1\rbrace\) ，也就有 \(A = \lbrace x\in\mathcal{X}: \pi(x) = 1\rbrace\) 。在这种情况下，我们也使用 \(\mathbb{P}_{x\sim \mathcal{D}}[\pi(x)]\) 来表达 \(\mathcal{D}(A)\) 。

\(L_{\mathcal{D},f}\) 的别称

\(L_{\mathcal{D},f}\) 又称作泛化误差（generalization error），风险（risk），\(h\) 的真正误差（true error of h）

A Note about The Information Available to The Learner

要注意的是，学习器本身并不知晓隐含的概率分布 \(\mathcal{D}\) 和 “完全正确” 的标记函数 \(f\) 。因此，学习器只能通过观察训练数据集，和环境交互，才能发现规律。

Summary

• 学习算法的输入和输出：一个学习算法接受一个训练集 \(S\) 作为输入，并且输出一个预测器（predictor） \(h_S: \mathcal{X} \rightarrow \mathcal{Y}\) 。其中，训练集 \(S\) 通过以下过程生成：首先从一个未知分布 \(D\) 中采样，然后使用目标函数（target function） \(f\) 标记。此外，预测器 \(h_S\) 的下标 \(S\) 强调了输出的 \(h_S\) 是依赖于 \(S\) 的。
• 学习算法的目标：学习算法的目标是找到一个 \(h_S\) ，关于未知分布 \(\mathcal{D}\) 和标记函数 \(f\) ，它能最小化误差。

Empirical Risk Minimization （ERM）

Empirical Error

由于学习器并不知道 \(\mathcal{D}\) 和 \(f\) ，因此，式（2.1）无法直接计算。学习器能够计算的是训练误差（training error），即分类器在训练数据上产生的误差，其定义如下： \[ L_S(h)\overset{def}{=}\frac{|\lbrace i\in[m]:h(x_i)\ne y_i \rbrace|}{m}\tag{2.2} \]

其中 \([m]=\lbrace 1,\dots ,m\rbrace\) 。

训练误差（training error）有时又称作经验误差（empirical error）或者经验风险（empirical risk）

ERM

既然学习算法能够从训练数据中获取关于这个世界的简要情况，所以寻找一个在训练数据上效果良好的答案是说得通的。寻找一个最小化 \(L_S(h)\) 的 \(h\) 的学习范式称作经验风险最小化（Empirical Risk Minimization），简称 ERM

The problem of ERM —— Overfitting

然而，ERM 可能会产生一种错误——过拟合。下面用一个例子说明。

过拟合的例子. Source:《Understanding Machine Learning: From Theory to Algorithms》

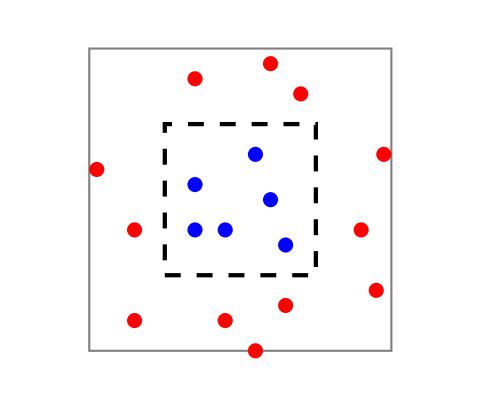
假设概率分布 \(\mathcal{D}\) 是灰色正方形框中的均匀分布，如果实例落在蓝色实例所在的黑色正方形框中，标记函数 \(f\) 将其标记为 1，否则标记为 0。考虑如下的预测器：

\[ h_S(x)= \begin{cases}y_i\quad &if\ \exists i\in[m]\ s.t. x_i=x;\\ 0\quad &ohterwise. \end{cases} \]

因为 \(h_S\) 在训练数据上，对实例标签的预测全部正确，所以 \(L_S(h_s) = 0\) 。根据经验风险最小化的原则，式子 （2.3）会被 ERM 选中（因为没有比 0 更小的训练损失）。然而如果取训练数据以外的一个点 \(x'\)，并且这个点在黑色正方形框中，那么根据式（2.3），\(h_S(x') = 0\) 。而实际上 \(f(x') = 1\)，这就会产生错误。

这种现象称作“过拟合”（overfitting）。直观的来说，当学习算法找到的假设太符合训练数据时，就会发生过拟合。

Empirical Risk Minimization with Inductive Bias

Applying ERM over a Restricted Search Space

一种常见的解决 ERM 过拟合的方法是限制 ERM 的搜索空间。规范的讲，在见到数据之前，学习器应该事先挑选出一个预测器集合。这个预测器集合又称作“假设类”（hypothesis class），记作 \(\mathcal{H}\) 。每一个 \(h\in \mathcal{H}\) 是一个 \(\mathcal{X}\rightarrow \mathcal{Y}\) 的函数。给定一个假设类 \(\mathcal{H}\) ，一个训练集 \(\mathcal{S}\) ，\(ERM_{\mathcal{H}}\) 学习器使用 ERM 规则来选取一个在 \(\mathcal{S}\) 上有最小可能误差的 \(h\) ，其中 \(h\in \mathcal{H}\) 。规范地，我们有如下公式： \[ ERM_{\mathcal{H}}(S)\in \underset{h\in \mathcal{H}}{argmin}(L_S(h)) \] 其中，\(argmin\) 表示在 \(\mathcal{H}\) 中使得 \(L_S(h)\) 最小的假设集合（\(h\in\mathcal{H}\)）。通过限制学习器从 \(\mathcal{H}\) 中选取预测器，学习器会偏向我们所特定的预测器集合。这种限制常常被称为归纳偏好（inductive bias）。由于这种限制的选择在学习器看到数据之前就确定了，因此在理想情况下，它应该基于一些有关所学问题的先验知识（prior knowledge）。

直观地，选择一个首先更多的假设类会更好地防止过拟合的发生，但是与此同时，这可能会导致一个更强的归纳偏好。

Finite Hypothesis Classes

对类的最简单的限制是设置一个其大小的上界（也就是，限制 \(\mathcal{H}\) 中预测器 \(h\) 的个数）。对应的，我们有如下结论：

• 只要有足够数量的训练样本，如果 \(\mathcal{H}\) 是一个有限的类（finite class），那么 \(ERM_{\mathcal{H}}\) 将不会产生过拟合。

那么至少需要多少训练样本呢？下面我们讨论这个问题

在此之前，我们先引入两个假设：

1. 可实现假设（The Realizability Assumption）：\(\exists h^\star \in \mathcal{H},\ L_{(\mathcal{D},f)}(h^\star) = 0\) 。
2. 独立同分布假设（The i.i.d. Assumption）：训练数据中每一个样本都关于分布 \(\mathcal{D}\) 独立同分布（independently and identically distributed，short for i.i.d.），记作 \(S\sim D^m\) 。其中， \(m\) 是 \(S\) 的大小，\(D^m\) 表示了根据 \(\mathcal{D}\) 采样 \(m\) 个元素，构成 \(m\) 元组，且每一个元素都独立于 \(m\) 元组其他元素

有关 可实现假设 和 独立同分布假设 的补充说明

• 可实现假设 暗示了在随机的训练样本 \(S\) ，\(S\) 由从 \(\mathcal{D}\) 中采样，又被 \(f\) 标记所得，\(L_S(h^\star) = 0\) 的可能性为 1。
• 独立同分布假设 表示每一个 \(S\) 中 \(x_i\) 都是全新地从 \(\mathcal{D}\) 中采样，并被 \(f\) 标记后生成的。

此外，定义 \(\delta\) 为取得一个不具代表性（nonrepresentative）的样本的概率，\(1-\delta\) 为预测行为的置信参数（confidence parameter）。

什么叫不具代表性（nonrepresentative）的样本？

• 这个样本不能代表实例的潜在规律。如一个水果本身很好吃，但是碰巧训练样本都是不好吃的，导致学习器学到了错误的结论。其中的不好吃的训练样本即是不具代表性的样本。

由于我们不能确保完美的标签预测，因此这里我们进一步引入另一个用来衡量预测效果的参数，即精度参数（accuracy parameter）。其通常记作 \(\epsilon\) 。我们用如下公式描述学习器是否获得成功：

• 事件 \(L_{(\mathcal{D},f)}(h_s)>\epsilon\) 表示学习器的失败
• 事件 \(L_{(\mathcal{D},f)}(h_S)\le \epsilon\) 表示学习器的近似成功。

令我们感兴趣的是，在由 \(m\) 个实例构成的 \(m\) 元组采样，会导致学习器失败的概率的上界。

规范的，记 \(S|_{x} = \lbrace x_1,\ \dots,\ x_m\rbrace\) 为训练数据的实例，我们希望找到下式的上界：

\[ \mathcal{D}(\lbrace S|_{x} : L_{(\mathcal{D},f)}(h_{S}) > \epsilon \rbrace) \]

记 \(\mathcal{H}_B\) 为“坏的”假设，即

\[ \mathcal{H}_B = \lbrace h\in\mathcal{H}: L_{(\mathcal{D},f)}(h) > \epsilon\rbrace \]

再令

\[ M = \lbrace S|_x : \exists h\in \mathcal{H}_B, L_S(h) = 0 \rbrace \]

显然，\(M\) 表示了误导学习器的样本集合。换句话说，对于每一个 \(S|_x \in M\) ，存在一个坏的假设，\(h\in \mathcal{H}_B\) ，但是在 \(S|_x\) 中它看上去是一个好的假设。

既然可实现假设表示存在 \(L_S(h_S) = 0\) ，因此，事件 \(L_{(\mathcal{D},f)}(h_s)>\epsilon\) 只可能在这种情况下发生：\(h\in \mathcal{H}_B\) ，但是 \(L_S(h) = 0\) 。也就是说，如果我们的采样样本在误导集合中，这种事件才会发生。因此，我们有：

\[ \lbrace S|_{x} : L_{(\mathcal{D},f)}(h_S) > \epsilon\rbrace \subseteq M \]

进一步的，\(M\) 可改写成：

\[ M = \underset{h\in \mathcal{H}_B}{\bigcup} \lbrace S|_x : L_S(h) = 0\rbrace \tag{2.5} \]

因此，

\[ \mathcal{D}^m(\lbrace S|_x : L_{(\mathcal{D},f)}(h_S) > \epsilon\rbrace) \le \mathcal{D}^m(M) = \mathcal{D}^m({\cup}_{h\in \mathcal{H}_B} \lbrace S|_x : L_S(h) = 0\rbrace) \tag{2.6} \]

利用 Union Bound 定理，可得：

\[ \mathcal{D}^m(\lbrace S|_x : L_{(\mathcal{D},f)}(h_S) > \epsilon\rbrace) \le \underset{h\in \mathcal{H}_B}{\sum}\mathcal{D}^m(\lbrace S|_x : L_S(h) = 0\rbrace)\tag{2.7} \]

定理（Union Bound）

• 对于两个集合 \(A\)，\(B\) 和分布 \(\mathcal{D}\) ，有 \[ \mathcal{D}(A\cup B) \le \mathcal{D}(A) + \mathcal{D}(B) \]

由于事件 \(L_S(h) = 0\) 等价于 \(\forall i, h(x_i) = f(x_i)\) ，所以，

\[ \mathcal{D}^m(\lbrace S|_x : L_S(h) = 0\rbrace) = \mathcal{D}^m(\lbrace S|_x : \forall i, h(x_i) = f(x_i) \rbrace) \]

又因为采样训练样本相互独立，且服从同一个分布 \(\mathcal{D}\) ，因此，

\[ \mathcal{D}^m(\lbrace S|_x : \forall i, h(x_i) = f(x_i) \rbrace) = \prod_{i=1}^{m}\mathcal{D}(\lbrace x_i : h(x_i) = f(x_i) \rbrace) \]

故有

\[ \mathcal{D}^m(\lbrace S|_x : L_S(h) = 0\rbrace) = \prod_{i=1}^{m}\mathcal{D}(\lbrace x_i : h(x_i) = f(x_i) \rbrace) \tag{2.8} \]

对于训练集中每一个独立的元素，有

\[ {D}(\lbrace x_i : h(x_i) = y_i \rbrace) = 1 - L_{(\mathcal{D},f)} \]

由于 \(L_{(\mathcal{D},f)}(h_s)>\epsilon\) ，故

\[ {D}(\lbrace x_i : h(x_i) = y_i \rbrace) = 1 - L_{(\mathcal{D},f)} \le 1 - \epsilon \]

利用 \(1-\epsilon \le e^{-\epsilon}\) 不等式对上式放缩，有

\[ {D}(\lbrace x_i : h(x_i) = y_i \rbrace) = 1 - L_{(\mathcal{D},f)} \le 1 - \epsilon \le e^{- \epsilon} \]

将上式带入式（2.8），有

\[ \mathcal{D}^m(\lbrace S|_x : L_S(h) = 0\rbrace)\le (1 - \epsilon)^m \le e^{- m\epsilon} \tag{2.9} \]

结合式（2.7），有

\[ \mathcal{D}^m(\lbrace S|_x : L_{(\mathcal{D},f)}(h_S) > \epsilon\rbrace) \le |\mathcal{H}_B|e^{- m\epsilon} \le |\mathcal{H}|e^{- m\epsilon} \]

设 \(\mathcal{D}^m(\lbrace S|_x : L_{(\mathcal{D},f)}(h_S) > \epsilon\rbrace) \le |\mathcal{H}|e^{- m\epsilon}< \delta\) ，则有

\[ m > \frac{log(\frac{|\mathcal{H}|}{\delta})}{\epsilon} \]

推导过程

\[ \delta > |\mathcal{H}|e^{-m\epsilon} \]

\[ log\delta > log|\mathcal{H}|-m\epsilon \]

\[ m\epsilon > log|\mathcal{H}| - log\delta \]

\[ m> \frac{log(\frac{|\mathcal{H}|}{\delta})}{\epsilon} \]

综上所述，有如下重要结论：

设 \(\mathcal{H}\) 为一个有限的假设类，令 \(\delta \in (0,1)\) ，\(\epsilon > 0\) ，\(m\) 为一个满足以下条件的整数： \[ m> \frac{log(\frac{|\mathcal{H}|}{\delta})}{\epsilon} \] 那么，对于任意的标记函数 \(f\) ，任意的分布 \(\mathcal{D}\) ，如果满足可实现假设（即，存在 \(h\in \mathcal{H}\) ，使得 \(L_{(\mathcal{D},f)}(h) = 0\)），则至少有 \(1-\delta\) 的可能性，在 \(S\) 上独立采样 \(m\) 个点，对于每一个 \(ERM\) 假设，满足如下式子： \[ L_{(\mathcal{D},f)}(h_S) \le \epsilon \]

这个结论意味着，只要有足够的训练数据（\(m> \frac{log(\frac{|\mathcal{H}|}{\delta})}{\epsilon}\)），在有限假设类上的 \(ERM_{\mathcal{H}}\) 会尽可能近似正确（其置信参数为 \(1-\delta\) ，最大的误差为 \(\epsilon\)）。

Reference

Shai Shalev-Shwartz, Shai Ben-David. Understanding Machine Learning: From Theory to Algorithms